Путешествие в мир программирования непременно приведет нас к фундаментальным принципам, которые лежат в основе эффективной работы кода. Одним из ярких примеров таких принципов является уникальная система кодирования, разработанная известными учеными Рида и Соломоном.
Код Рида-Соломона – это искусно выдержанное сочетание математических алгоритмов и практических реализаций, позволяющих достичь невероятных результатов в области обработки информации. Это средство является одним из самых мощных инструментов, позволяющих обеспечить надежность и стойкость передачи данных.
Основная идея этого подхода заключается в применении комбинации различных методов для проверки и восстановления целостности информации. В результате, код Рида-Соломона позволяет обнаруживать ошибки, восстанавливать поврежденные данные, а также обнаруживать и исправлять ошибки в ходе передачи информации. Причем, это происходит с высокой степенью надежности и эффективности, что делает эту систему незаменимой в многочисленных отраслях современной информационной сферы.
Что такое код Рида-Соломона и его применение

Код Рида-Соломона является системой коррекции ошибок, которая позволяет обнаруживать и исправлять ошибки в передаваемых данных. Он основан на алгоритме, разработанном Исаком Ридом и Густавом Соломоном в 1960-х годах.
Используя принципы линейной алгебры, код Рида-Соломона представляет исходные данные в виде блоков, называемых символами, и добавляет дополнительные символы, называемые проверочными символами. Затем эти символы кодируются и записываются в виде матрицы или таблицы.
Основной принцип кода Рида-Соломона заключается в том, что даже в случае возникновения ошибок при передаче данных, он способен обнаружить эти ошибки и восстановить исходные данные, используя информацию, содержащуюся в проверочных символах.
Применение кода Рида-Соломона широко распространено в сфере хранения и передачи цифровых данных. Например, он часто используется для защиты информации на компакт-дисках, DVD, в цифровых сетях передачи данных, а также в цифровом видео и аудио технологиях.
| Пример | Расширенное применение |
| Защита данных на компакт-дисках | Медицинская диагностика |
| Цифровое видео | Сетевые технологии |
| Цифровая фотография | Информационная безопасность |
Основные идеи и преимущества алгоритма Рида-Соломона

Преимуществом кода Рида-Соломона является его способность предоставлять избыточность информации, тем самым повышая сохранность данных при возникновении ошибок передачи. Благодаря использованию математического подхода, этот алгоритм обеспечивает высокую степень корректировки ошибок и предоставляет возможность восстановить потерянные данные на основе имеющейся информации.
Код Рида-Соломона обеспечивает достаточно большое количество возможных комбинаций вариантов ошибок, что делает его идеальным решением для передачи данных в условиях шумового канала. Алгоритм позволяет распределить информацию на части и автоматически восстановить потерянные данные, что гарантирует целостность контента и его воспроизводимость без потерь.
Другим замечательным преимуществом кода Рида-Соломона является его универсальность. Он может быть успешно применен в различных областях, таких как цифровые коммуникации, хранение данных, системы обнаружения и исправления ошибок. Более того, этот алгоритм может быть использован для проверки и защиты целостности данных, что гарантирует безопасность и достоверность информации.
В современном информационном обществе, где цифровые данные играют значительную роль, использование кода Рида-Соломона представляет собой надежный и эффективный метод обработки информации. Его основные принципы и преимущества сделали этот алгоритм одним из наиболее популярных и широко применяемых в сфере телекоммуникаций и вычислительной техники.
Структура кода Рида-Соломона и его математические основы
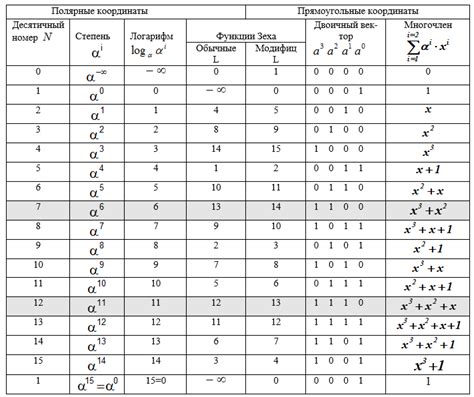
В данном разделе мы рассмотрим основную структуру и математические аспекты кода Рида-Соломона, алгоритма, который широко используется для обработки и защиты информации. Мы рассмотрим, как этот код устроен и какие математические принципы лежат в его основе.
Прежде чем углубиться в подробности, давайте взглянем на общую идею кода Рида-Соломона. Он основан на использовании математических операций для разделения данных на фрагменты и добавления дополнительной информации для восстановления и проверки целостности. Такой подход позволяет обеспечить надежность и коррекцию ошибок в передаваемых или хранимых данных.
Структура кода Рида-Соломона включает в себя генерацию специального набора кодовых слов, которые состоят из исходных данных и дополнительной корректирующей информации. Эти кодовые слова затем разделяются на несколько фрагментов и передаются или сохраняются независимо друг от друга.
Одной из основных математических основ кода Рида-Соломона является поле Галуа. Это алгебраическая структура, которая позволяет производить операции сложения, вычитания, умножения и деления на конечном наборе элементов. Поле Галуа является основой для генерации кодовых слов и выполнения операций коррекции ошибок.
Код Рида-Соломона также использует полиномиальную арифметику, основанную на поле Галуа, для выполнения операции умножения и деления. Это позволяет создавать кодовые слова с правильно настроенными коэффициентами, которые обеспечивают эффективную коррекцию ошибок и восстановление исходных данных.
Процесс кодирования и декодирования при использовании кода Рида-Соломона

- Генерация кодовых символов:
- Формирование блоков данных:
- Передача и хранение закодированных данных:
- Декодирование и восстановление данных:
В первом этапе происходит генерация кодовых символов с помощью алгоритма Рида-Соломона. Этот алгоритм использует различные математические операции, такие как полиномиальные деления и сложения, для создания специальных символов, называемых кодовыми символами. Эти символы служат для проверки и восстановления данных при наличии ошибок.
Второй этап заключается в разделении исходных данных на блоки определенного размера и их кодировании. Каждый блок состоит из оригинальных данных и нескольких кодовых символов. Количество кодовых символов зависит от требуемого уровня коррекции ошибок. Блоки данных формируются таким образом, чтобы обеспечить возможность восстановления данных в случае их повреждения.
Закодированные блоки данных могут быть переданы по сети или записаны на носитель информации. Этот этап очень важен, так как он гарантирует сохранность данных и обеспечивает возможность восстановления информации в случае возникновения ошибок.
При декодировании происходит проверка целостности и восстановление данных. В случае, если данные были повреждены в процессе передачи или хранения, код Рида-Соломона позволяет найти и исправить ошибки. Для этого используется сложный математический алгоритм, который основывается на кодовых символах, введенных на предыдущих этапах.
Алгоритмы возможной обнаружения и исправления ошибок с применением кода Рида-Соломона
Первый алгоритм, который будет рассмотрен, - метод обнаружения ошибок. Он позволяет определить, есть ли ошибки в полученных данных. Для этого используются различные математические операции и сравнения. Алгоритм сканирует полученные данные и ищет нарушения в структуре кодовых слов, что указывает на возможное наличие ошибок. В результате применения этого алгоритма можно получить информацию о наличии ошибок и их расположении в данных.
Второй алгоритм, который будет рассмотрен в данном разделе, - метод исправления ошибок. Он используется для восстановления исходных данных, если были обнаружены ошибки. Этот алгоритм основан на использовании дополнительной информации, которая была добавлена в кодированное сообщение с помощью кода Рида-Соломона. Алгоритм анализирует нарушения в структуре кодовых слов и пытается восстановить исходные данные на основе этих данных и дополнительной информации, которая содержит информацию о возможных ошибках.
Оба этих алгоритма важны для эффективного применения кода Рида-Соломона. Они позволяют не только обнаруживать возможные ошибки, но и исправлять их, что обеспечивает высокий уровень надежности при передаче и хранении данных. В следующих разделах статьи будут рассмотрены подробности работы каждого из этих алгоритмов с примерами и объяснением математических операций, используемых при их выполнении.
Примеры практического применения алгоритма Рида-Соломона

Один из основных применений кода Рида-Соломона - это исправление ошибок передачи данных. Код Рида-Соломона может обнаружить и исправить ошибки, возникающие в процессе передачи данных по ненадежному каналу связи. Примером такой ситуации может быть передача данных через беспроводную сеть, где сигнал может подвергаться искажению и помехам. Алгоритм позволяет восстановить исходные данные даже при наличии определенного количества ошибок в переданной информации.
Код Рида-Соломона также успешно применяется в системах хранения данных, особенно там, где надежность и безопасность являются приоритетными задачами. Например, он может использоваться в различных типах носителей информации, включая жесткие диски, флеш-накопители и цифровые архивы. Этот алгоритм позволяет предотвратить потерю данных и восстановить информацию при ее повреждении.
Другим примером практической реализации кода Рида-Соломона является его применение в системах передачи видео и аудиоданных. Благодаря этому алгоритму можно обеспечить стабильность и непрерывность потока данных, минимизируя возможные потери кадров или артефакты на звуке. Таким образом, код Рида-Соломона способствует более плавному и качественному просмотру или прослушиванию мультимедийного контента.
| Примеры практического применения кода Рида-Соломона: |
|---|
| Исправление ошибок передачи данных |
| Надежное хранение данных на носителях |
| Стабильная передача видео и аудиоданных |
Комплексные системы кодирования и декодирования с применением алгоритма Рида-Соломона
Данный раздел посвящен подробному рассмотрению процесса кодирования и декодирования с использованием сложных систем, основанных на алгоритме Рида-Соломона. Вместо принципов работы исследуется механизм функционирования таких систем.
Кодирование и декодирование
При исследовании кодов Рида-Соломона рассматривается метод кодирования информации с использованием корректирующих кодов. Коды Рида-Соломона позволяют повысить устойчивость передачи и хранения данных, а также обеспечить их целостность.
Важное преимущество кодов Рида-Соломона заключается в том, что они способны обнаруживать и исправлять ошибки в передаваемых данных, а также обеспечивать надежную защиту от искажений. Данный алгоритм основывается на математических принципах, изучаемых в теории кодирования и декодирования.
Системы кодирования и декодирования
Реализация комплексных систем кодирования и декодирования с использованием кода Рида-Соломона предусматривает использование различных алгоритмов для обработки данных. Важным компонентом таких систем являются генераторы и проверители кодов, которые обеспечивают надежность и корректность передачи информации.
Комплексные системы кодирования и декодирования с применением кодов Рида-Соломона находят применение в различных областях, включая передачу данных по неканалам связи с высоким уровнем помех и ошибок, хранение информации на надежных носителях, а также в криптографии и системах безопасности.
Вопрос-ответ

Какие принципы лежат в основе работы кода Рида-Соломона?
Принципы работы кода Рида-Соломона основаны на алгебраических методах обработки информации и предназначаются для обнаружения и исправления ошибок при передаче данных через неприводимые полиномы.
Каким образом код Рида-Соломона корректирует ошибки при передаче данных?
Код Рида-Соломона использует принципы коррекции ошибок на основе добавления дополнительной информации, известной как проверочные символы, к передаваемым данным. При получении данных, декодер может использовать эти проверочные символы для обнаружения и исправления ошибок.
Какие преимущества имеет код Рида-Соломона по сравнению с другими методами обработки ошибок?
Код Рида-Соломона обладает высокой степенью коррекции ошибок и обнаружения, что делает его особенно полезным в условиях ненадежных каналов связи. Он также широко используется в цифровых хранилищах, где надежность и целостность данных являются критически важными.
Какова математическая основа кода Рида-Соломона?
Код Рида-Соломона основан на полиномиальной алгебре. Он использует операции сложения и умножения над полиномами для обработки данных и проверки на наличие ошибок. Неприводимые полиномы играют важную роль в данном коде, так как определяют его корректирующую способность и устойчивость к ошибкам.



