Предел последовательности – это важное понятие в математике, которое позволяет определить, к какому числу стремится последовательность чисел.
Если предел последовательности существует и равен определенному числу а, его обозначают как lim an = a. Это означает, что при увеличении номера элемента последовательности значения элементов последовательности становятся ближе к числу а.
Для того чтобы определить предел последовательности, нужно использовать строгие математические определения и понятия, которые позволяют точно определить, к чему стремятся элементы последовательности.
Что такое предел последовательности?

Формально, предел последовательности a_n при n стремящемся к бесконечности равен числу a, если для любого положительного числа e, существует такое номер N, что для всех n > N выполняется неравенство: |a_n - a|
Предел последовательности играет ключевую роль в анализе и позволяет решать различные математические задачи, связанные с непрерывностью функций, суммированием рядов и многими другими.
| Пример: | Рассмотрим последовательность а_n = 1/n. Её предел при n стремящемся к бесконечности равен нулю, так как значения элементов последовательности приближаются к нулю при увеличении номеров. |
Понятие предела последовательности

Для того чтобы доказать существование предела последовательности, необходимо показать, что для любого положительного числа ε существует такой номер n0, начиная с которого все элементы последовательности находятся в пределах от ε до -ε относительно предела. Если это условие выполняется, говорят о сходимости последовательности.
Свойства предела последовательности

1. Единственность предела: У последовательности может быть только один предел. Если последовательность имеет предел, то он единственный.
2. Арифметические свойства: Пусть lim an = A и lim bn = B. Тогда:
a) lim (an + bn) = A + B
b) lim (an - bn) = A - B
c) lim (an * bn) = A * B
d) Если B ≠ 0, то lim (an / bn) = A / B
3. Ограниченность последовательности: Если последовательность имеет предел, то она ограничена.
4. Сходящаяся последовательность: Последовательность является сходящейся, если у нее есть конечный предел.
Как определить предел последовательности?

Для определения предела последовательности нужно проанализировать поведение элементов последовательности по мере их роста. Предел последовательности обозначается как lim an = a, что означает, что при n стремящемся к бесконечности элементы последовательности тенденционно приближаются к числу a.
Существуют различные методы определения предела последовательности, включая методы сходимости, расходимости, оценки предела. Для точного определения предела необходима математическая точность в анализе каждого элемента последовательности.
В таблице ниже приведены основные признаки определения предела последовательности:
| Метод | Описание |
| Метод сходимости | Последовательность стремится к пределу постепенно и устойчиво. |
| Метод расходимости | Последовательность не имеет предела, элементы рассходятся. |
| Метод оценки предела | Определение предела с помощью оценки поведения элементов последовательности. |
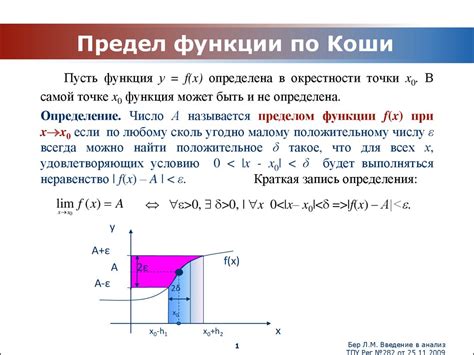
Предел последовательности по Коши
Предел последовательности по Гейне

Предел последовательности по Гейне определяется как a, если для любого элемента ε > 0 найдется такое натуральное число N, что для всех натуральных чисел n > N выполняется условие |an - a|
Таким образом, пределом по Гейне является число a, к которому стремится последовательность при достаточно больших номерах элементов.
Вопрос-ответ

Как определить предел последовательности при стремлении к бесконечности?
Для определения предела последовательности при стремлении к бесконечности необходимо рассмотреть поведение последовательности на бесконечности и сравнить его с искомым пределом. Если последовательность стремится к определенному числу при увеличении n до бесконечности, то этот число и будет являться пределом последовательности.
Что означает условие lim an = a для последовательности?
Условие lim an = a означает, что предел последовательности an при n, стремящемся к бесконечности, равен числу a. Это означает, что если мы возьмем значения элементов последовательности на бесконечности, и они будут все ближе к числу a, то число a и будет пределом данной последовательности.



