Одним из важных аспектов математики является определение принадлежности точки функции. Этот вопрос возникает при решении различных задач, связанных с графиками функций, анализом данных и моделированием.
Существует несколько способов определения того, принадлежит ли точка заданной функции. Один из наиболее распространенных методов - подстановка координат точки в уравнение функции и проверка выполняющегося равенства. Также можно использовать графический метод, при котором строится график функции и проверяется, лежит ли точка на этом графике.
Мастерство в определении принадлежности точки функции чрезвычайно важно при решении математических задач и имеет практическое применение во многих областях науки и техники.
Основные методы определения
Для определения принадлежности точки функции можно использовать следующие основные методы:
1. Метод подстановки: подставить координаты точки в уравнение функции и проверить равенство.
2. Метод графический: построить график функции и увидеть, лежит ли точка на графике.
3. Метод числовых интервалов: исследовать значения функции в окрестности точки и сравнить с заданной координатой.
Графический метод на плоскости
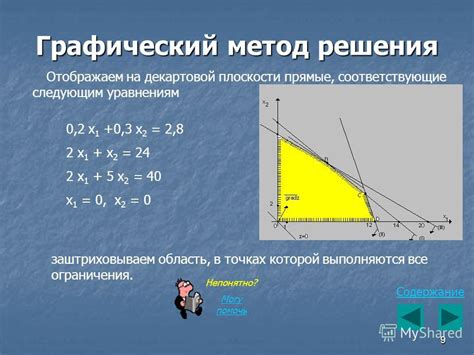
Аналитический метод: подстановка значения

Аналитический метод: использование формулы
Для определения принадлежности точки к функции с помощью аналитического метода необходимо использовать математические формулы. Для этого подставляют координаты точки (x, y) в уравнение функции и проверяют выполнение равенства.
Например, если дано уравнение функции y = x^2 и точка (2, 4), то подставляя x = 2 в уравнение, получим y = 2^2 = 4. Таким образом, точка (2, 4) принадлежит функции y = x^2.
Использование производной
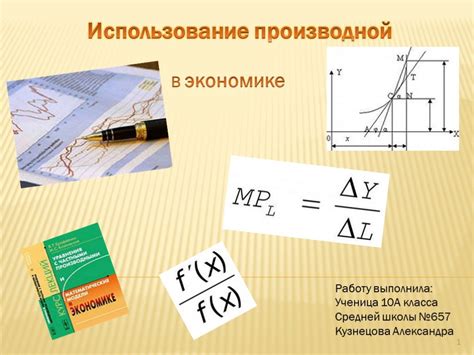
Для использования производной необходимо сначала найти аналитическую формулу производной функции. После этого можно вычислять значение производной в конкретной точке, чтобы определить ее поведение. Производная является мощным инструментом при анализе функций и может помочь определить множество важных характеристик функции в заданной точке.
Использование теоремы Лагранжа
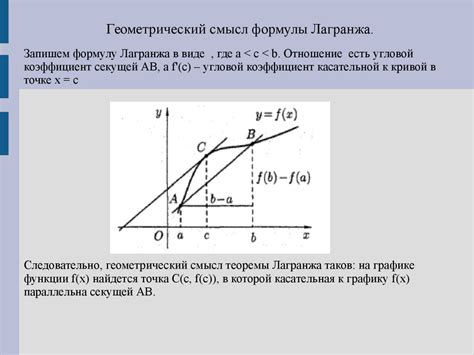
Метод последовательных приближений

Для применения метода последовательных приближений необходимо выбрать начальное приближение точки функции, затем построить итерационный процесс, в котором текущее приближение точки используется для вычисления следующего приближения. Итерационный процесс продолжается до тех пор, пока не будет достигнута необходимая точность или заданное число итераций.
Метод последовательных приближений широко применяется в различных областях науки и техники, где требуется приближенное решение уравнений или систем уравнений, например, в численном анализе, физике, экономике и многих других областях.
Метод половинного деления

Принцип метода заключается в поиске отрезка, на концах которого знаки функции различны. Затем отрезок делится пополам и выбирается тот подотрезок, на концах которого знаки функции различны. Этот процесс повторяется до достижения заданной точности.
Метод половинного деления гарантирует сходимость к корню уравнения, но может быть неэффективным при маленькой скорости сближения.
Метод Ньютона

Идея метода Ньютона заключается в следующем: выбирается начальное приближение к корню уравнения, затем вычисляется значение функции и ее производной в этой точке. Далее делается корректировка приближения в соответствии с направлением, определяемым производной. Этот процесс повторяется до тех пор, пока не будет достигнута заданная точность.
Метод Ньютона имеет высокую скорость сходимости, но при этом требует наличия производной функции и хорошего начального приближения. Некоторые функции могут иметь несколько корней или неточности из-за особенностей функции.
Сравнение методов и их эффективность
Определение принадлежности точки функции можно осуществить различными методами, такими как метод подстановки, графический метод и табличный метод.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Метод подстановки | Прост в использовании | Требует времени на подстановку |
| Графический метод | Позволяет визуально представить решение | Не всегда точен |
| Табличный метод | Позволяет систематизировать данные | Может быть сложен для больших объемов информации |
Выбор метода определяется конкретной задачей, требуемой точностью и объемом данных. Эффективность метода также зависит от характеристик функции и специфики задачи.
Примеры решения задач по методам определения

Пример 1:
- Задача: Определить, принадлежит ли точка (-2, 3) функции y = 2x + 1.
- Решение: Подставим координаты точки в уравнение функции: y = 2*(-2) + 1 = -4 + 1 = -3.
- Ответ: Точка (-2, 3) не принадлежит функции y = 2x + 1, так как y не равно 3.
Пример 2:
- Задача: Проверить, принадлежит ли точка (0, -4) графику функции y = x^2 - 4x.
- Решение: Подставим координаты точки в уравнение функции: y = 0^2 - 4*0 = 0 - 0 = 0.
- Ответ: Точка (0, -4) не принадлежит графику функции y = x^2 - 4x, так как y не равно -4.
Вопрос-ответ

Какие методы можно использовать для определения принадлежности точки функции?
Для определения принадлежности точки функции можно использовать графический метод, аналитический метод, а также метод замены переменных. Графический метод основан на построении графика функции и определении положения точки относительно графика. Аналитический метод заключается в подстановке координат точки в уравнение функции и проверке выполняется ли это уравнение. Метод замены переменных позволяет свести задачу к анализу функции с более удобными координатами.
Как определить, принадлежит ли точка графику функции?
Чтобы определить, принадлежит ли точка графику функции, нужно подставить координаты этой точки в уравнение функции. Если полученное уравнение верно, то точка принадлежит графику функции, если нет - то не принадлежит.
Как можно использовать метод замены переменных для определения принадлежности точки функции?
Метод замены переменных можно использовать для определения принадлежности точки функции, заменяя исходные переменные на другие, более удобные. После этого преобразования можно провести анализ функции с более удобными координатами и определить, принадлежит ли точка функции.
Что такое графический метод определения принадлежности точки функции?
Графический метод определения принадлежности точки функции основан на построении графика функции и определении положения точки относительно этого графика. Если точка лежит на графике функции, то она принадлежит функции, если точка не пересекает график или находится вне него, то не принадлежит.



