Понятие о пересекающихся и параллельных прямых
Геометрия - одна из основ математики, основанная на изучении фигур, их свойств и взаимного расположения. Одним из ключевых понятий в геометрии является понятие прямой. Прямая - это линия, состоящая из точек, которые лежат на одной и той же прямой. При этом существует интересное свойство прямых - они могут пересекаться или быть параллельными.
Параллельные прямые
Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, то есть расстояние между ними в любой точке одинаково. Такое положение прямых является ключевым в геометрии и находит широкое применение в различных областях, от строительства и архитектуры до теории относительности и геодезии.
Почему прямые не пересекаются
Геометрия и ее основы
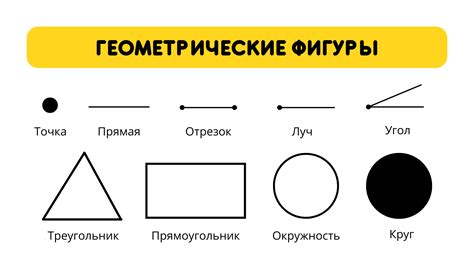
Одним из основных постулатов геометрии является принцип, что через две различные точки можно провести одну и только одну прямую. Этот постулат гарантирует, что две прямые, не пересекаются, если они параллельны. Параллельные прямые имеют постоянное расстояние между собой и никогда не пересекаются.
| Основное понятие | Описание |
| Точка | Нетмерная, бесконечно мала область пространства. |
| Линия | Множество точек, не имеющих ширины и длины. |
| Плоскость | Множество точек, образующих плоскую поверхность. |
| Угол | Образованные двумя лучами, исходящими из общего начала. |
| Фигура | Форма, образованная линиями, плоскостями и т.д. |
Уникальные свойства прямых
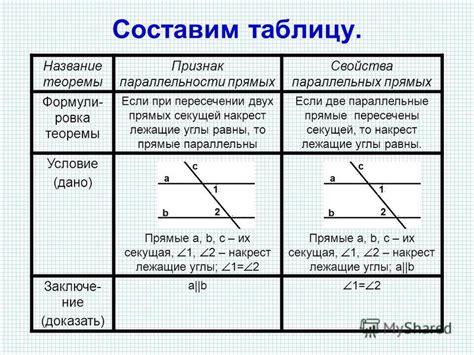
Две прямые, которые не пересекаются, остаются параллельными на всем их протяжении. Это важное следствие аксиомы Евклида, которая гласит, что через точку вне прямой можно провести только одну параллельную прямую. Именно это свойство приводит к образованию параллельных линий и плоскостей, которые играют важную роль в геометрии и ее приложениях.
Как это влияет на геометрию

| Прямая | Свойства |
| Пересекающиеся | Образуют углы, имеют общие точки, могут пересекаться |
| Непересекающиеся | Параллельны, не имеют общих точек, не пересекаются |
Основные теоремы геометрии
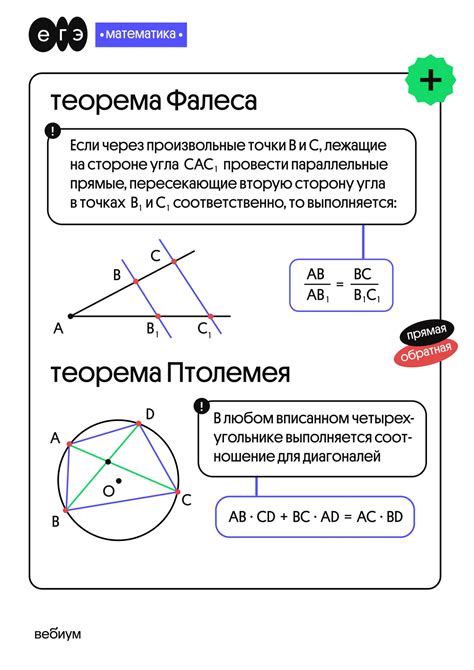
В геометрии существует ряд основных теорем, которые играют важную роль при решении задач и построении пространственных моделей. Некоторые из них включают в себя:
1. Теорема Пифагора, утверждающая, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
2. Теорема о трёх перпендикулярах, утверждающая, что три перпендикуляра, проведенные из вершин треугольника к противолежащим сторонам, пересекаются в одной точке.
3. Теорема Фалеса, утверждающая, что если две параллельные прямые пересекают треугольник, то точки пересечения лежат на одной прямой.
4. Теорема о прямых, пересекающих сюжет, утверждающая, что прямые, проходящие через две точки одной плоскости, не пересекают сюжет этой плоскости.
Эти и другие теоремы позволяют более глубоко понимать геометрию и используются при решении различных задач и физических моделей.
Построение геометрических фигур
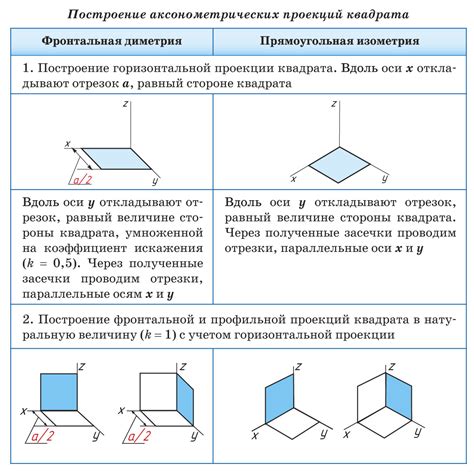
Геометрические фигуры могут быть построены на основе различных примитивных элементов, таких как точки, линии и углы. Основные фигуры, такие как треугольники, квадраты и круги, могут быть построены с использованием простых геометрических операций.
Для построения треугольника, например, необходимо провести три несекущиеся прямые линии, соединяющие три различные точки. Для построения квадрата нужно провести четыре прямые линии, каждая из которых должна быть перпендикулярна двум смежным сторонам. Круг может быть построен как множество всех точек, равноудаленных от центра этого круга.
Построение геометрических фигур является важным шагом в изучении математики и развитии аналитических навыков. Оно помогает понять свойства различных фигур и их взаимосвязи, а также применить их в реальных задачах и ситуациях.
Прямые в пространстве
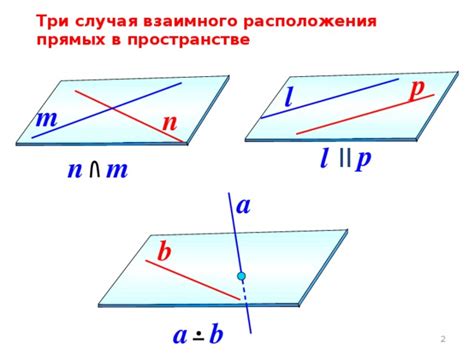
В трехмерном пространстве две прямые могут быть расположены по-разному. Однако, если две прямые не параллельны и не лежат на одной плоскости, то они обязательно пересекутся в одной точке. Это свойство называется аксиомой о единственности прямой, проходящей через две точки.
Если же прямые параллельны, то они не пересекаются и расположены на одинаковом расстоянии друг от друга на протяжении бесконечности. Это свойство влияет на геометрию пространства и означает, что параллельные прямые никогда не сойдутся в одной точке.
Вопрос-ответ

Почему две параллельные прямые не пересекаются?
Две параллельные прямые не пересекаются, потому что они лежат на одной плоскости и имеют одинаковый наклон. Если прямые имели бы разный наклон, они бы обязательно пересеклись в какой-то точке. Когда прямые параллельны, они идут в одном направлении и никогда не сходятся.
Какое значение имеет свойство параллельности прямых для геометрии?
Свойство параллельности прямых имеет большое значение в геометрии. Оно используется при построении различных фигур, расчете углов и длин отрезков, а также при решении различных задач. Параллельные прямые позволяют делать точные измерения и упрощают решение геометрических задач.
Как две параллельные прямые влияют на углы в геометрических фигурах?
Если две прямые параллельны, то углы между ними будут равны друг другу. Это свойство часто используется при решении задач на построение геометрических фигур и определение их свойств. Параллельные прямые позволяют делать точные измерения углов и создавать симметричные фигуры.
Какие примеры использования параллельных прямых можно привести из повседневной жизни?
Параллельные прямые можно встретить в повседневной жизни в различных ситуациях. Например, линии на дороге, строения на зданиях, решетка на окне, рамки на окне и т.д. Параллельные прямые используются для создания симметричных и гармоничных форм в архитектуре, дизайне и других областях.



