Понятие дифференцируемости функции в точке является одним из ключевых понятий математического анализа. Дифференцируемость функции в точке означает, что функция имеет производную в данной точке, то есть существует некоторый предельный коэффициент изменения функции, который можно определить аналитически.
Концепция дифференцируемости позволяет нам понять поведение функции в окрестности определенной точки, выявить экстремумы функции и определить направление ее изменения. При изучении дифференцируемости функции в точке важно учитывать не только существование производной, но и ее непрерывность в данной точке.
Дифференцируемость функции в точке является одним из основных инструментов анализа функций и позволяет проводить более глубокое и точное исследование их свойств. Понимание этого понятия поможет вам углубить свои знания в математике и применить их на практике в решении различных задач и проблем.
Что такое дифференцируемость функции

Формально, функция \( f(x) \) дифференцируема в точке \( x = a \), если существует конечный предел:
\[
f'(a) = \lim_{{h \to 0}} \frac{{f(a + h) - f(a)}}{{h}}
\]
где \( f'(a) \) – производная функции \( f(x) \) в точке \( x = a \).
Основные понятия и определения

Перед тем как погружаться в изучение дифференцируемости функции в точке, необходимо понимать некоторые базовые понятия:
| Функция | – это правило, которое каждому элементу одного множества (аргументу) ставит в соответствие элемент другого множества (значение). |
| Точка | – это элемент множества, на котором определена функция. |
| Дифференцируемость | – свойство функции, показывающее, насколько она гладко меняется в данной точке. Если функция дифференцируема в точке, то ее приращение можно аппроксимировать линейной функцией. |
Теперь, имея понимание этих основных понятий, переходим к изучению дифференцируемости функции и ее свойств в конкретной точке.
Условия дифференцируемости функции в точке

Функция \( f(x) \) считается дифференцируемой в точке \( x = a \), если у нее существует производная в этой точке \( f'(a) \).
Для того чтобы функция была дифференцируемой в точке \( a \), необходимо чтобы она была непрерывной в этой точке. То есть, чтобы производная существовала, функция должна быть определена и непрерывна в окрестности точки \( a \).
Кроме того, функция должна гладко меняться в окрестности точки \( a \), что означает, что ее поведение вблизи точки дифференцирования должно быть однозначным и не иметь резких скачков.
Геометрический смысл дифференцируемости
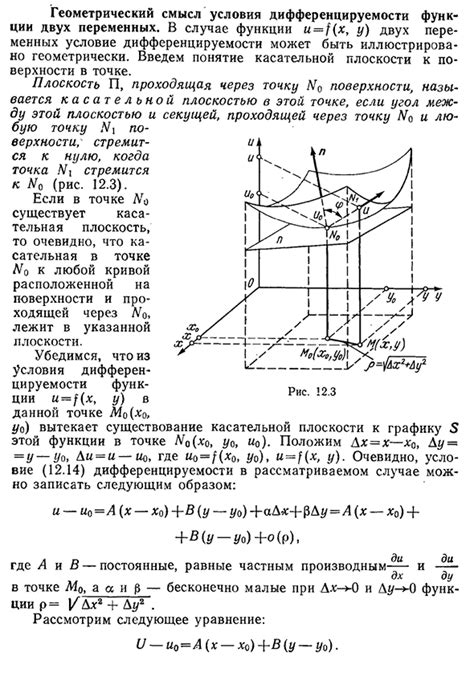
Понятие дифференцируемости функции в точке имеет глубокий геометрический смысл. Если функция дифференцируема в точке, то это означает, что в данной точке график функции имеет касательную, которая хорошо приближает поведение функции в окрестности этой точки.
Более точно, если функция дифференцируема в точке x=a, то существует некоторая прямая (касательная), которая касается графика функции в точке (a, f(a)) таким образом, что ее угловой коэффициент равен значению производной функции в этой точке.
Таким образом, дифференцируемость функции в точке позволяет локально аппроксимировать поведение функции с помощью прямой, что имеет важное значение в геометрии и анализе функций.
Касательная к графику функции
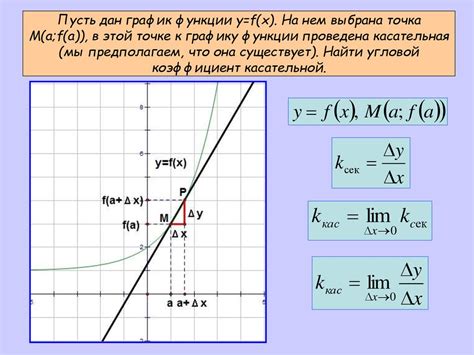
Примеры дифференцируемых функций

- Линейная функция f(x) = ax + b, где a и b - константы.
- Квадратичная функция f(x) = ax^2 + bx + c, где a, b и c - константы.
- Синусоидальная функция f(x) = sin(x) или косинусоидальная функция f(x) = cos(x).
Эти функции имеют производные в каждой точке своего домена, что означает их дифференцируемость.
Формулы дифференцирования
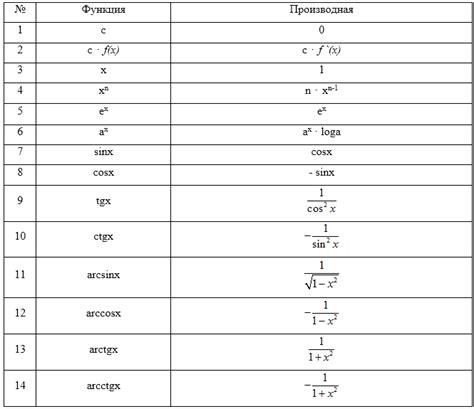
Дифференцирование функций в точке может быть осуществлено с помощью следующих формул:
| 1. Если \(f(x) = k\), где \(k\) - константа, то \(f'(x) = 0\). |
| 2. Правило для константы: \((kf(x))' = kf'(x)\). |
| 3. Правило для суммы: \((f(x) + g(x))' = f'(x) + g'(x)\). |
| 4. Правило для произведения: \((f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\). |
| 5. Правило для частного: \(\left(\frac{f(x)}{g(x)} ight)' = \frac{f'(x)\cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}\) (для \(g(x) eq 0\)). |
Примеры недифференцируемых функций

Несмотря на то, что большинство функций, с которыми мы сталкиваемся, обладают свойством дифференцируемости, существуют и функции, которые недифференцируемы в определенных точках. Некоторые из таких примеров включают:
| Функция | Причина недифференцируемости |
|---|---|
| Модульная функция | Функция |x| имеет разрыв в точке x=0, поэтому не является дифференцируемой в этой точке. |
| Функция Хевисайда | Функция Хевисайда (единичная ступенька) имеет разрыв в точке x=0, что делает ее недифференцируемой в этой точке. |
| Функция Вейерштрасса | Функция Вейерштрасса является примером непрерывной, но нигде недифференцируемой функции. |
Разрывы и узлы функций

Важно уметь определять разрывы и узлы функций, так как они могут влиять на поведение функции в окрестности данных точек. Кроме того, понимание характера разрывов помогает правильно проводить анализ функций и оптимизировать их поведение.
Вопрос-ответ

Что такое дифференцируемость функции в точке?
Дифференцируемость функции в точке означает, что в этой точке функция имеет производную. Это означает, что функция достаточно гладкая и положение касательной к графику функции определено. Однако дифференцируемость функции в точке не гарантирует ее дифференцируемость на всем интервале.
Как проверить дифференцируемость функции в точке?
Для того чтобы узнать, дифференцируема ли функция в точке, необходимо вычислить производную функции в этой точке. Если значение производной существует, то функция дифференцируема в данной точке. Также можно использовать определение дифференцируемости через приращение функции и приращение аргумента.



