Точка - одно из основных понятий геометрии, представляющее собой объект без объема и размеров. Точка обладает лишь позицией в пространстве и не имеет никаких измеримых характеристик. Однако именно точки являются основными элементами, на основе которых строится вся геометрия.
В геометрии точка обозначается заглавной буквой латинского алфавита, например, точка A. Для того чтобы указать позицию точки в пространстве, необходимо задать ее координаты. В двумерном пространстве координатами точки служат два числа - абсцисса и ордината. В трехмерном пространстве добавляется еще одна координата - аппликата.
Основное свойство точек заключается в том, что через любые две различные точки можно провести прямую. Это свойство является базовым для построения геометрических фигур и решения задач. Точки могут быть расположены как на одной прямой, так и в пространстве, их положение является фундаментальным понятием геометрии.
Что представляет собой точка в геометрии?

Точка может быть представлена как на плоскости, так и в трехмерном пространстве. Она является основным строительным блоком геометрии и используется для определения расстояний и направлений между другими геометрическими объектами. Точка не имеет объема, поэтому ее нельзя измерить в пространстве. Однако точки используются для построения более сложных геометрических фигур и участков.
Смысл и понятие точки

Основное свойство точки - ее положение в пространстве. Точка может быть определена с помощью координат или описана относительно других точек.
В геометрии точка служит основным строительным элементом для построения линий, плоскостей и фигур, а также для формулирования основных аксиом и постулатов.
Математическое описание точки

Основные свойства точки
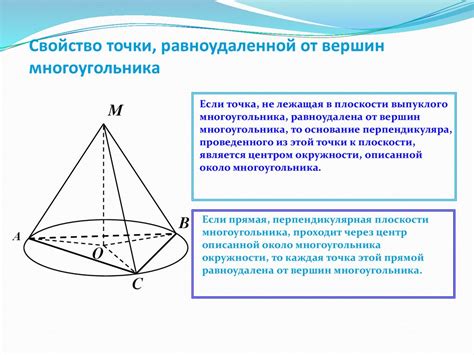
1. Местоположение: Точка не имеет никаких размеров, она лишь характеризует положение в пространстве.
2. Описание: Точку можно задать с помощью ее координат или через определение местоположения относительно других точек.
3. Название: Точка обозначается заглавной латинской буквой, например, A, B, C и т.д.
4. Связь: Две точки можно соединить прямой линией, а несколько точек образуют фигуры и объекты, такие как линии, многоугольники и другие.
Нулевые размеры и понятие положения
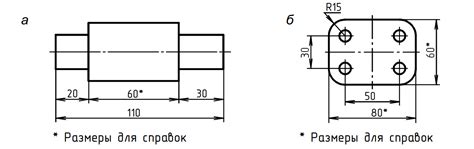
Местоположение точки определяется её координатами на плоскости или в пространстве. В двумерном пространстве точку можно задать двумя числами (x, y), где x – координата по горизонтали, y – координата по вертикали. В трёхмерном пространстве каждая точка имеет три координаты (x, y, z) – по трем координатным осям.
Точка с нулевыми размерами является основой для построения других фигур, таких как отрезки, линии, многогранники. Даже имея нулевые размеры, точка играет важную роль в геометрии и используется для определения расстояний, углов, иных характеристик геометрических объектов.
Уникальность и неделимость

Неделимость точки означает, что она представляет собой абстрактное понятие, не имеющее внутренней структуры или частей. В геометрии точка рассматривается как математическая абстракция, задающая позицию в пространстве без физического объема или формы. Поэтому точку нельзя разделить на части или представить как объект с конкретными размерами.
Использование точек в геометрии
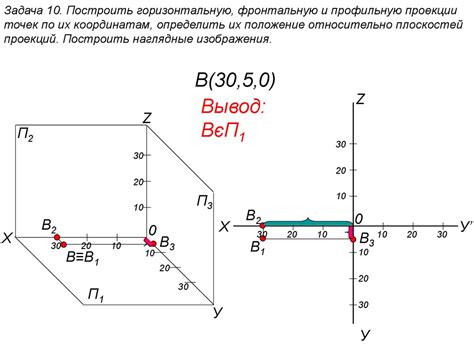
Точки могут быть соединены отрезками, линиями или плоскостями, что позволяет создавать геометрические фигуры различной формы и размера. Они также используются для определения расстояний, углов и других характеристик геометрических объектов.
Важно понимать, что точка в геометрии не имеет размеров и не занимает объема, она представляет собой идеальное математическое понятие, используемое для упрощения математических вычислений и анализа пространственных отношений.
Структуры и отрезки на плоскости
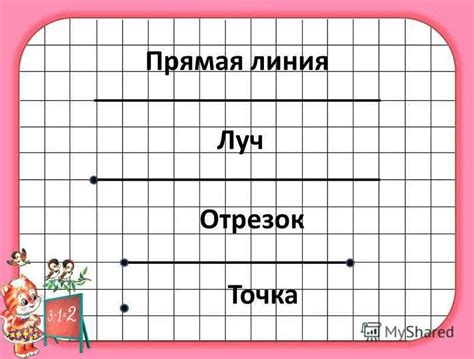
В геометрии точка представляет собой абстрактное понятие без размеров и объема, выражающее позицию или положение объекта в пространстве. Для описания отрезков, линий и других геометрических объектов используются структуры, состоящие из точек.
Отрезок на плоскости представляет собой часть прямой между двумя точками. Он имеет длину и направление, определенные координатами точек, между которыми он лежит. Отрезок можно описать с помощью координат его конечных точек и уравнения прямой, на которой он расположен.
Вопрос-ответ

Что такое точка в геометрии?
Точка в геометрии - это понятие, обозначающее местоположение в пространстве без размеров и объемов. Точка не имеет ни длины, ни ширины, ни высоты, она является абстрактным объектом, который используется для определения линий, плоскостей и других геометрических фигур.
Какие свойства имеет точка в геометрии?
Точка в геометрии обладает несколькими свойствами, включая то, что через любые две различные точки можно провести прямую, что точка не имеет никаких измерений, и что любые три точки, не лежащие на одной прямой, образуют плоскость.
Может ли точка быть видимой на плоскости или в пространстве?
Точка в геометрии является абстрактным понятием и не имеет физических измерений, поэтому она не может быть видимой, как, например, отрезок или круг. Тем не менее, мы можем обозначать точки на плоскости или в пространстве с помощью координат или графических обозначений.
Какую роль играют точки в геометрии?
Точки являются основными элементами геометрии и используются для построения других геометрических фигур, таких как отрезки, линии, плоскости и многогранные тела. Они служат начальным материалом для построения всех остальных объектов геометрии.
Можно ли провести линию через одну единственную точку?
По определению, через одну единственную точку можно провести бесконечное количество прямых. Точка является начальным элементом для построения линий и плоскостей, поэтому провести линию через точку - этот вопрос не имеет смысла в математическом контексте.



