Построение ориентированного графа из матрицы смежности является важным этапом в анализе и визуализации сложных систем и структур. При этом необходимо учитывать различные методы и подходы к данной задаче, чтобы эффективно работать с графовыми данными и получать информацию из них.
Матрица смежности представляет собой таблицу, показывающую связи между вершинами графа. При этом она может быть как ненаправленной, так и ориентированной. В данной статье рассмотрим способы построения ориентированного графа на основе матрицы смежности и алгоритмы работы с ним.
Изучив различные методы и подходы управления графами, мы сможем более глубоко понять структуру данных и использовать их в различных областях, таких как социальные сети, транспортные системы, биоинформатика и многое другое.
Методы построения ориентированного графа
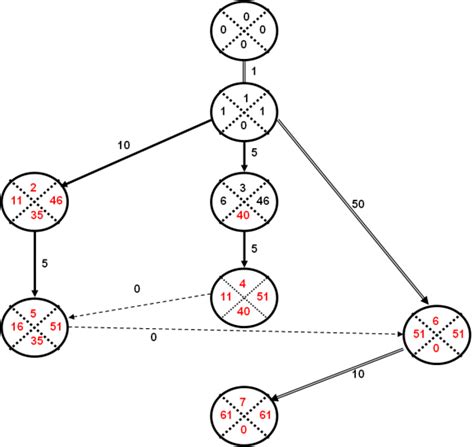
Построение ориентированного графа из матрицы смежности может быть осуществлено различными методами, в зависимости от задачи и характеристик данных. Некоторые из методов включают в себя:
- Прямой перебор всех элементов матрицы смежности и добавление соответствующих рёбер в граф.
- Использование алгоритмов обхода графа (например, поиск в глубину или в ширину) для построения ориентированного графа.
- Использование оптимизированных алгоритмов, основанных на структуре матрицы смежности, для более эффективного построения графа.
Выбор метода построения ориентированного графа зависит от конкретных требований и особенностей исходных данных.
Алгоритм построения

Для построения ориентированного графа из матрицы смежности можно использовать следующий алгоритм:
- Создать пустой граф G.
- Пройти по всем элементам матрицы смежности.
- Если значение элемента на позиции i, j больше нуля, то добавить ребро из вершины i в вершину j в граф G.
- Продолжить этот процесс для всех элементов матрицы.
Таким образом, после завершения алгоритма мы получим ориентированный граф, построенный на основе матрицы смежности.
Выбор структуры графа

При построении ориентированного графа из матрицы смежности важно правильно выбрать структуру графа, которая отражает особенности данных и бизнес-задач. Существуют различные методы и подходы к выбору структуры графа, каждый из которых имеет свои особенности и применимость.
Один из основных критериев при выборе структуры графа является назначение самого графа – для анализа сети дорог, связей между людьми или технологических процессов. Для каждого случая следует выбирать подходящую структуру графа, которая соответствует особенностям и специфике предметной области.
Также при выборе структуры графа важно учитывать сложность алгоритмов, которые будут выполняться на этом графе, а также требования к производительности системы. Некоторые структуры графа могут быть оптимальными для определенных видов анализа, в то время как другие могут быть более универсальными, но требовательными к вычислительным ресурсам.
| Метод/Подход | Описание |
|---|---|
| Список смежности | Представление графа в виде списка вершин с указанием смежных вершин. Позволяет эффективно хранить разреженные графы. |
| Матрица смежности | Представление графа в виде матрицы, где значение элемента указывает наличие или отсутствие ребра между вершинами. Удобно для быстрого доступа к данным. |
Выбор структуры графа зависит от конкретных задач и требований к системе, поэтому важно подходить к этому процессу внимательно и обдуманно, чтобы обеспечить эффективность анализа и высокую производительность системы.
Матрица смежности для построения графа
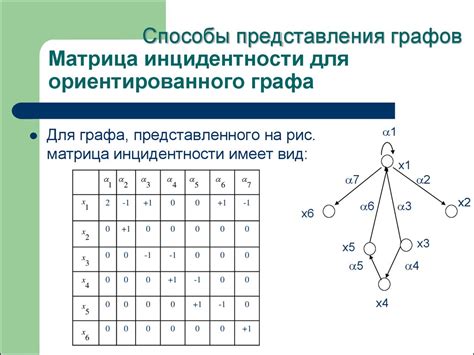
При использовании матрицы смежности для построения ориентированного графа, ее формат может быть различным в зависимости от того, является ли граф направленным или ненаправленным. Для ориентированного графа можно хранить только информацию о направлении ребер, добавляя в матрицу смежности значения 1 для соответствующих элементов.
Преимуществом использования матрицы смежности является простота представления и быстрый доступ к информации о смежных вершинах. Однако этот метод может быть неэффективен для больших графов из-за большого объема памяти, необходимого для хранения квадратной матрицы.
Преобразование матрицы

Матрица смежности представляет собой простой способ представления графа в виде матрицы.
Для построения ориентированного графа из матрицы смежности необходимо преобразовать матрицу таким образом, чтобы учесть направленность ребер.
В случае ориентированного графа матрица смежности будет представлять собой квадратную матрицу, где значение элемента m[i][j] будет равно весу ребра из вершины i в вершину j.
Для каждой пары вершин i и j, если существует ребро из вершины i в вершину j, то в соответствующей ячейке матрицы будет указана величина веса ребра.
Если же ребра из вершины i в вершину j нет, то соответствующая ячейка матрицы останется нулевой или будет содержать другой признак отсутствия связи.
Преобразование матрицы смежности в ориентированный граф позволяет четко задать направленность ребер и удобно проводить анализ структуры графа.
Определение вершин и ребер

Чтобы определить вершины, достаточно рассмотреть строки и столбцы матрицы смежности. Каждая строка и столбец соответствует одной вершине, их количество равно размеру матрицы. Взаимное положение элементов матрицы позволяет определить наличие ребер между вершинами.
Ребро между вершинами существует, если соответствующий элемент в матрице смежности не равен нулю. Если граф ориентированный, то направление ребра определяется позицией элемента (i, j) в матрице.
Таким образом, определение вершин и ребер в матрице смежности является первым шагом к построению ориентированного графа.
Теоретические аспекты построения графа
При построении ориентированного графа из матрицы смежности необходимо учитывать основные принципы теории графов. Граф представляет собой абстрактную модель, состоящую из вершин и ребер, связывающих их. В ориентированном графе каждое ребро имеет направление, что отличает его от неориентированного графа.
Основными элементами графа являются вершины (узлы) и ребра (стрелки). В матрице смежности вершины графа представляются в строках и столбцах. Элементы матрицы могут быть наполнены значениями 0 и 1, где 1 указывает на наличие ребра между соответствующими вершинами, а 0 - на отсутствие связи.
При построении ориентированного графа из матрицы смежности важно учитывать направление ребер и корректное преобразование матричных данных в графическое представление. Это позволит получить надежную модель взаимосвязей между элементами графа и эффективно анализировать его структуру и свойства.
Свойства ориентированного графа
1. Направление рёбер: В ориентированном графе каждое ребро имеет направление от одной вершины к другой. Это позволяет учитывать направленность связей между вершинами и моделировать различные виды отношений.
2. Исходящая степень вершины: Исходящая степень вершины определяет количество рёбер, которые выходят из данной вершины. Это важное свойство, которое позволяет анализировать поток информации или влияния от данной вершины.
3. Входящая степень вершины: Входящая степень вершины указывает на количество рёбер, входящих в данную вершину. Это может быть полезным при анализе зависимостей и источников информации для конкретной вершины.
4. Циклы и пути: В ориентированном графе могут присутствовать различные типы циклов и путей, которые позволяют анализировать зацикленность и направленность путей между вершинами.
5. Транзитивные связи: Ориентированный граф позволяет отображать транзитивные отношения между вершинами, где одна вершина связана с другой через промежуточные вершины. Это позволяет моделировать сложные зависимости и взаимодействия в графе.
Использование графа в анализе данных

Графы представляют собой мощный инструмент для анализа данных в различных областях, таких как социальные сети, транспортные системы, биоинформатика и т.д. В анализе данных графы позволяют моделировать различные взаимосвязи между объектами и анализировать их с использованием различных алгоритмов.
Одним из основных преимуществ использования графов в анализе данных является возможность представления сложных структурных связей между данными и проведения разнообразных аналитических исследований на основе этих связей.
Алгоритмы обхода графа, поиска кратчайших путей, выявления сообществ и центральных узлов позволяют выявлять скрытые закономерности и структуры в данных, делая графы универсальным инструментом для анализа сложных систем и данных.
Вопрос-ответ

Какой метод используется для построения ориентированного графа из матрицы смежности?
Для построения ориентированного графа из матрицы смежности часто применяют методы обхода матрицы и установки соответствующих ребер между вершинами графа в зависимости от значений элементов матрицы.
Какие подходы можно использовать для преобразования матрицы смежности в ориентированный граф?
Существует несколько подходов к преобразованию матрицы смежности в ориентированный граф: от простого прохода по матрице с установкой направления ребра в соответствии с ее значением до более сложных алгоритмов, учитывающих выделение особых структур графа.



