В мире информационных технологий, где каждый нюанс может иметь огромное значение, эффективность обработки данных становится ключевым фактором для достижения успеха. И одним из фундаментальных инструментов, которые позволяют достичь высокой эффективности обработки данных, является построение оптимальной схемы на основе Списка Дизъюнкций Нормальной Формы (СДНФ).
СДНФ - это метод логического анализа и представления булевых функций, позволяющий преобразовывать сложные логические выражения в более простые. Он основывается на комбинации элементарных логических операций - конъюнкции и отрицания, что позволяет представить любую булеву функцию в виде дизъюнкции.
Один из главных преимуществ построения схемы по СДНФ - возможность оптимизации и минимизации ресурсов, требуемых для обработки данных. Это позволяет значительно ускорить процессы вычислений и снизить нагрузку на систему. Однако, чтобы достичь ожидаемых результатов, необходимо придерживаться определенных шагов и учесть некоторые важные указания.
Основные принципы формирования структуры алгебраической формулы в СДНФ
При построении схемы по системе дизъюнктивных нормальных форм (СДНФ) важно придерживаться ряда главных принципов, которые помогут создать эффективную и логичную структуру алгебраической формулы. В этом разделе мы рассмотрим основные инструкции, которые предоставят вам ценные советы и помогут сделать шаги в правильном направлении.
- Анализ логической функции: Прежде чем приступать к построению схемы, необходимо тщательно проанализировать логическую функцию, исследовать ее структуру и свойства. Для этого можно использовать различные методы, такие как таблицы истинности, логические графы или булевы алгебры. Это позволит получить полное представление о функции и определить главные элементы, на которых будет основываться схема.
- Минимизация логической функции: После анализа и понимания логической функции, следует приступить к процессу минимизации формулы. Минимизация помогает упростить выражение, удалив избыточные термины и комбинируя одинаковые или взаимоисключающиеся элементы. Это позволяет существенно сократить размер схемы и повысить ее эффективность.
- Разработка структуры схемы: На основе минимизированной логической функции следует разработать структуру схемы. Основное правило здесь - сохранение простоты и понятности. Рекомендуется использовать блочное представление, где каждый блок отвечает за выполнение определенных логических операций (И, ИЛИ, НЕ и др.). Правильное размещение блоков и их взаимодействие сильно влияют на эффективность и читаемость схемы.
- Выбор элементов схемы: При выборе элементов схемы следует ориентироваться на их функциональные возможности и компактность. Использование элементов, которые соответствуют условиям задачи и позволяют эффективно реализовать логические операции, поможет создать оптимальную схему. Кроме того, важным фактором является применение стандартных элементов, которые легко доступны и имеют документированную спецификацию.
- Проверка и оптимизация схемы: После завершения построения схемы следует ее тщательно проверить на соответствие и требованиям задачи, а также на наличие возможных ошибок. В процессе проверки можно произвести оптимизацию схемы, исключив ненужные элементы или внесшие дублирование блоки. Это позволит сократить количество используемых элементов и повысить производительность схемы.
Следуя вышеперечисленным принципам при построении схемы по системе дизъюнктивных нормальных форм (СДНФ), вы сможете разработать эффективную и компактную структуру, которая будет удовлетворять требованиям задачи и облегчать реализацию логических операций.
Понимание сути СДНФ и ее применение в логических функциях

СДНФ представляет собой логическую формулу, состоящую из элементарных логических конъюнкций. Она позволяет перевести сложные и запутанные логические функции в более простые формы, что упрощает их анализ и восприятие.
Применение СДНФ в логических функциях позволяет разложить сложные выражения на набор элементарных отдельных конъюнкций, что значительно упрощает понимание функции и ее работы. Это дает возможность проанализировать функцию пошагово, рассмотреть каждую конъюнкцию отдельно и определить ее вклад в общий результат.
Таким образом, понимание сути СДНФ и умение ее применять в логических функциях становятся важными навыками для тех, кто занимается анализом и оптимизацией различных процессов, которые можно представить в виде логических функций. Данный инструмент позволяет разбить сложные выражения на более простые компоненты и более глубоко понять, как работает функция в целом.
Поиск всех элементарных следствий для Сокращенной дизъюнктивной нормальной формы (СДНФ)

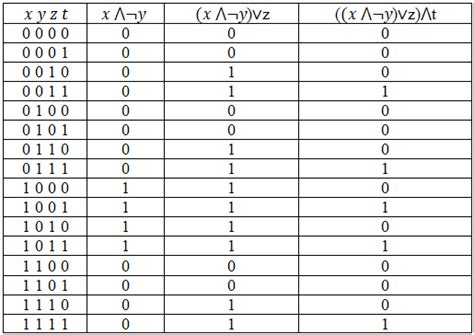
Для начала, необходимо построить таблицу истинности для заданной логической функции. Таблица истинности будет содержать все возможные комбинации значений входных переменных и соответствующее значение функции.
| Входные переменные | Значение функции |
|---|---|
| 0 0 | 1 |
| 0 1 | 0 |
| 1 0 | 1 |
| 1 1 | 1 |
Затем, мы исследуем строки в таблице, где значение функции равно 1. Эти строки указывают, что данная литералная конъюнкция является импликантом, так как она покрывает одну или несколько строк с значением 1. Каждый столбец, в котором присутствует литерал 0, может быть заменен на символ "B" (don't care) для дальнейшего упрощения. Также, строки с общими нулями между литералами можно объединить.
Продолжая этот процесс, мы можем найти все простые импликанты для заданной логической функции. Простые импликанты могут быть представлены в виде конъюнкций литералов, где каждый литерал соответствует значению входных переменных. Путем анализа таблицы истинности и объединения строк с общими "don't care" символами, мы можем выделить все возможные простые импликанты для заданной функции.
Отбор оптимальных базисных инверсий для уменьшения СДНФ

В данном разделе мы рассмотрим методику отбора наиболее оптимальных базисных инверсий для минимизации сложности СДНФ. Будут представлены ключевые этапы и советы по выбору эффективных простых импликант, которые позволят получить более компактную формулу логического выражения.
Процесс отбора оптимальных простых импликант является важной задачей при разработке эффективных схем логического проектирования. Для достижения минимального размера СДНФ необходимо учитывать различные факторы, такие как число включенных переменных, частота их использования, а также возможность выражения через другие более компактные базисные инверсии.
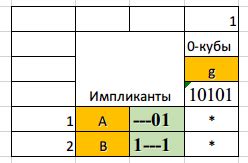
Ключевой этап выбора оптимальных простых импликант состоит в построении таблицы импликантности, которая позволяет оценить значимость каждой возможной импликанты посредством учета числа включенных переменных и их взаимодействия. На основе анализа этой таблицы, можно выделить наиболее значимые базисные инверсии исходной СДНФ.
| Импликанта | Включенные переменные | Число переменных | Значимость |
|---|---|---|---|
| Импликанта 1 | Переменная 1, Переменная 2 | 2 | Средняя |
| Импликанта 2 | Переменная 1, Переменная 3 | 2 | Высокая |
| Импликанта 3 | Переменная 2, Переменная 3 | 2 | Средняя |
Следующим шагом является отбор наиболее значимых базисных инверсий на основе полученных данных в таблице импликантности. Учитывая потенциальную возможность выражения через комбинацию других импликант, рекомендуется выбирать базисные инверсии с наибольшей значимостью и минимальным количеством переменных.
Импликанты, которые не могут быть выражены через комбинацию других импликант, считаются необходимыми для сохранения полной функциональности исходного логического выражения. При минимизации СДНФ следует предотвращать избыточное использование таких "незаменимых" импликант, так как это может привести к увеличению размера выражения без улучшения его функциональности.
Обратная задача состоит в поиске таких комбинаций импликант, которые позволят выразить одну через набор других для уменьшения размера СДНФ. Однако, стоит отметить, что в процессе минимизации необходимо учитывать ограничения на сложность самой схемы и использование дополнительных логических элементов.
Правильный выбор оптимальных простых импликант является основой для создания компактной СДНФ, что в свою очередь упрощает разработку более эффективных логических схем. Следуя указанным советам и методикам, можно получить наиболее оптимальный результат в минимизации сложности СДНФ.
Построение таблицы истинности и выбор соответствующих импликант
Для эффективного построения схемы по СДНФ необходимо провести анализ логической функции и составить таблицу истинности. Таблица истинности позволяет определить все возможные комбинации значений входных переменных и соответствующие значения функции. Затем из этой таблицы можно выделить необходимые импликанты, которые будут использованы при построении схемы.
Основной шаг в построении таблицы истинности - это перебор всех комбинаций значений входных переменных и определение соответствующих значений функции. Для этого необходимо определить количество входных переменных и составить все возможные комбинации их значений, приписывая каждой комбинации соответствующее значение функции. Таким образом, получается таблица, в которой столбцы соответствуют значениям входных переменных, а последний столбец - значениям функции.
После построения таблицы истинности необходимо проанализировать ее структуру и выбрать необходимые импликанты. Импликанты являются непосредственными множителями функции и позволяют выразить функцию в СДНФ. Для выбора импликантов следует обратить внимание на строки таблицы, в которых функция принимает значение 1. Эти строки соответствуют комбинациям значений входных переменных, при которых функция истинна. Таким образом, все такие строки являются потенциальными импликантами, которые могут быть использованы при построении схемы.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В данном примере строки 2, 3, 5 и 6 таблицы истинности соответствуют значениям функции, равным 1. Эти строки являются импликантами и могут быть использованы при построении схемы.
Логические операции: ключ к упрощению СДНФ

Разбор Совершенно Дизъюнктивной Нормальной Формы (СДНФ) может быть сложной задачей, но с помощью правильного применения логических операций вы сможете значительно упростить этот процесс. В данном разделе мы рассмотрим различные методы и стратегии, которые помогут вам эффективно манипулировать логическими выражениями с целью получения более простой и понятной СДНФ.
Первым шагом в упрощении СДНФ является анализ выражения и выделение общих логических операций. Простейший метод - использование операций конъюнкции (И), дизъюнкции (ИЛИ) и инверсии (НЕ). При помощи этих операций вы можете комбинировать и объединять логические выражения, что позволяет сократить количество термов и переменных.
Другим важным аспектом является применение дистрибутивных и де Моргановых законов. Дистрибутивный закон позволяет распространять операцию ИЛИ по закону дистрибутивности, а закон де Моргана позволяет изменять операции И и ИЛИ с помощью инверсии. Правильное использование этих законов может значительно сократить сложность логического выражения и упростить его форму.
Наконец, не забывайте о приоритете операций. Правильное определение порядка применения операций может значительно повлиять на конечный результат. Выделите главные операции, определите их приоритет и с количеством переменных проанализируйте, как можно объединить их для упрощения.
Используя логические операции и знание основных законов, вы сможете значительно сократить сложность СДНФ и упростить ее форму. Постепенно разрабатывайте свою стратегию и экспериментируйте с различными методами, чтобы достичь наиболее оптимального и понятного результата.
Оптимизация результатов и проверка полученной логической формулы в Дизъюнктивной Нормальной Форме (ДНФ)

После построения логической формулы в ДНФ, важно проверить ее корректность и оптимизировать для достижения наилучших результатов. В данном разделе мы рассмотрим основные принципы проверки и оптимизации полученной схемы в ДНФ.
Первым шагом является проверка алгоритмической правильности логической формулы. Необходимо убедиться, что каждая переменная входит в формулу ровно один раз, а все переменные участвуют в выражении. Также важно проверить соответствие полученного результата исходным данным и провести тестирование на различных наборах входных значений.
Оптимизация полученной схемы в ДНФ позволяет сократить количество логических элементов и упростить процесс обработки данных. Одним из основных способов оптимизации является использование алгебры логики для упрощения выражений. Для этого можно применять правила ассоциативности, дистрибутивности, поглощения и другие логические преобразования.
Дополнительным методом оптимизации является объединение подобных по структуре и значению логических элементов, что позволяет сократить количество элементов, снизить задержку сигнала и улучшить общую производительность схемы. Важно также избегать избыточности и повторений логических элементов.
При оптимизации схемы важно учесть требования к скорости работы и потребляемой мощности. Можно использовать специализированные алгоритмы для оптимизации схемы в зависимости от поставленных задач. Также следует обратить внимание на возможность применения мультиплексоров и других комбинационных схем для дальнейшего сокращения числа логических элементов и улучшения эффективности схемы.
Вопрос-ответ

Какая цель статьи "Постройте эффективную схему по СДНФ: простые шаги и советы"?
Целью статьи является описание простых шагов и советов по построению эффективной схемы с использованием СДНФ (сокращенной дизъюнктивной нормальной формы).
Что такое СДНФ и зачем ее использовать при построении схемы?
СДНФ (сокращенная дизъюнктивная нормальная форма) - это логическая форма, используемая для описания функции в виде суммы произведений. При построении схемы, СДНФ позволяет упростить логическую функцию и сделать ее более эффективной.



