Как мы воспринимаем и анализируем информацию, окружающую нас? Каждый день мы сталкиваемся с множеством данных, но как мы можем быть уверены в их достоверности? Каким образом мы можем решать сложные задачи, основываясь на имеющихся фактах? Возможно, одним из ответов на эти вопросы является применение математического инструмента, известного как формула Байеса.
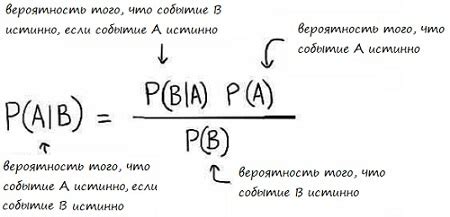
Формула Байеса, разработанная в XVIII веке английским математиком Томасом Байесом, является одним из основных инструментов теории вероятностей. Она позволяет оценить вероятность события, основываясь на имеющихся данных и априорной информации. Но зачем нам такая формула и как она может быть применена?
Например, представьте, что вам необходимо принять решение о том, каким образом вам добраться до дома, используя общественный транспорт. У вас есть две возможности: автобус и метро. Вы знаете, что автобусы приходят регулярно и водители пунктуальны, но иногда возникают пробки на дорогах. С другой стороны, метро ходит по расписанию, но возможны перебои в работе по техническим причинам. Каким образом вы можете определить, какой вид транспорта будет наиболее надежным для вашего конкретного случая?
Введение в понятие определения формулы Байеса
| Вероятностное событие | Статистическое событие |
| Независимые события | Зависимые события |
| Условные вероятности | Оценка вероятности события |
В контексте определения формулы Байеса, основное внимание уделяется связи между вероятностными и статистическими событиями, а также способам вычисления условных вероятностей. Размерность вероятностей и их взаимоотношения находятся в основе этого математического инструмента и отражаются в формуле Байеса. Понимание и применение этого метода позволяет проводить различные статистические исследования, оценивать вероятность возникновения событий и принимать решения на основе имеющихся данных.
Реальные ситуации, где формула Байеса находит применение
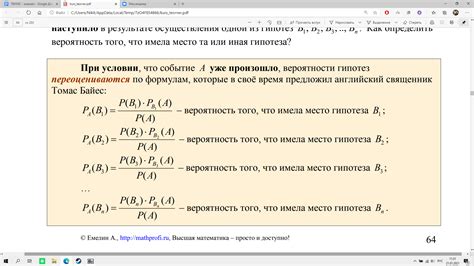
Одной из областей применения формулы Байеса является медицина. Врачи используют эту формулу при диагностировании болезней и определении вероятности наличия определенного заболевания у пациента. Например, предположим, у пациента есть симптомы, которые могут быть индикатором определенного заболевания. Формула Байеса позволяет оценить вероятность наличия этого заболевания, исходя из вероятности появления симптомов у больных и здоровых людей.
Другим примером применения формулы Байеса является область искусственного интеллекта, в частности, обработка естественного языка. При автоматической обработке текстов алгоритмы могут использовать формулу Байеса для анализа вероятности того, какие слова могут встречаться вместе и как эти связи помогают определить смысл текста.
В сфере маркетинга формула Байеса может быть использована для предсказания вероятности конверсии клиента или потребителя. Например, компания, основываясь на вероятности действий и предпочтений клиента, может определить, насколько вероятна покупка или другое желаемое действие.
В заключении, формула Байеса - это неотъемлемый инструмент для оценки вероятностей в различных областях. Она позволяет учесть контекст и предыдущую информацию, что помогает прогнозировать и принимать эффективные решения в условиях неопределенности.
Разнообразные сферы, где возможно применение теории вероятностей Байеса

| Область | Примеры применения |
|---|---|
| Медицина | Диагностика заболеваний на основе симптомов, оценка эффективности лечения, прогнозирование и управление пациентами |
| Финансы | Оценка рисков, принятие решений о вложении капитала, прогнозирование финансовых показателей |
| Технологии и исследования | Распознавание образов, рекомендательные системы, анализ данных, машинное обучение |
| Бизнес и маркетинг | Прогнозирование спроса, определение вероятности успеха нового продукта, персонализация предложений |
| Криминалистика | Судебная экспертиза, анализ улик, прогнозирование вероятности совершения преступлений |
Кроме того, формула Байеса может быть использована в планировании и оптимизации процессов, в принятии решений, в политическом анализе и во многих других областях. Благодаря своей гибкости и возможности учета новых данных, этот подход чрезвычайно полезен и эффективен в современном мире.
Вопрос-ответ

Что такое формула Байеса?
Формула Байеса – это математическая формула, которая позволяет пересчитывать вероятности событий на основе новой информации.
Как можно применить формулу Байеса в повседневной жизни?
Формула Байеса может быть применена для определения вероятности различных событий, таких как диагностика болезней, фильтрация спама в электронной почте, предсказание погоды и другие задачи с вероятностным характером.
Каким образом формула Байеса влияет на машинное обучение?
Формула Байеса является одной из основных концепций машинного обучения. Она позволяет обновлять вероятностные модели на основе новых данных и считается основой для алгоритмов классификации и регрессии.
В каких областях науки и техники применяется формула Байеса?
Формула Байеса находит широкое применение в различных областях, включая статистику, искусственный интеллект, компьютерные науки, экономику, физику, медицину и другие. Она используется для прогнозирования, классификации, анализа данных и многих других задач.
Можете привести пример использования формулы Байеса для принятия решений в бизнесе?
Конечно! Допустим, у нас есть интернет-магазин, и мы хотим предсказать вероятность покупки товара определенным клиентом. Мы можем использовать формулу Байеса, чтобы обновить предварительные вероятности на основе новых данных, таких как история покупок клиента, его рейтинги и мнения других пользователей. Таким образом, мы сможем принимать более обоснованные решения при проведении маркетинговых кампаний и оптимизации работы магазина.
Какую формулу использует Байес?
Байес использует формулу, известную как формула Байеса или теорема Байеса. Формула Байеса используется для вычисления вероятности одного события, основываясь на информации о других событиях.



