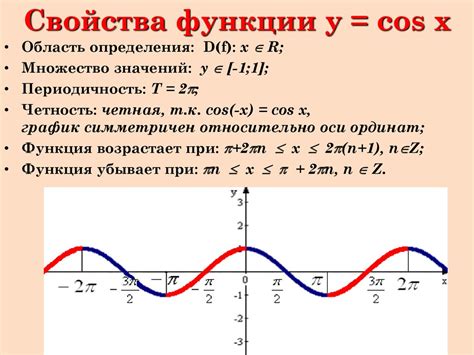
Функция у cos x является одной из основных тригонометрических функций и имеет важное значение в математике и физике. Она представляет собой косинус угла x, где x - это аргумент функции, выраженный в радианах. График функции у cos x представляет собой периодическую волнообразную кривую, которая повторяется каждые 2π радиан.
Для понимания того, принадлежит ли графику функции у cos x, необходимо оценить диапазон изменения функции. Косинусное значение функции у cos x лежит в интервале от -1 до 1. Таким образом, график функции у cos x всегда ограничен внутри прямоугольника со сторонами, параллельными осям координат и вершинами в точках (-1, -1), (-1, 1), (1, 1) и (1, -1).
Итак, график функции у cos x принадлежит ограниченному диапазону значений и всегда ограничен прямоугольником с координатами вершин. Это позволяет легко определить форму и характер изменения функции у cos x на графике.
Утверждение о графике функции cos x
Выявление особенностей функции
Для определения особенностей функции у cos x необходимо анализировать её график. Особенности функции могут включать в себя точки экстремума, точки перегиба, асимптоты и другие характеристики. Проведя исследование графика функции, можно определить её поведение, интервалы возрастания и убывания, а также точки экстремума. Это поможет более полно понять характеристики функции и использовать их при решении различных задач.
Математические принципы

Проверка гипотезы
Для того чтобы определить, принадлежит ли графику функции у cos x, необходимо проверить условия гипотезы. Проверка может осуществляться путем анализа уравнения функции, нахождения ее области определения и области значений, а также рассмотрения ее графика. Также можно провести дополнительные исследования, такие как вычисление производной функции или анализ поведения функции в разных точках.
Рассмотрение графика функции y = cos x
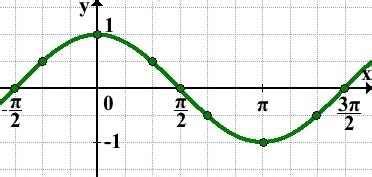
График функции y = cos x представляет собой периодическую кривую, которая колеблется между значениями -1 и 1. Функция cos x имеет период 2π, что означает, что график повторяется через каждые 2π радиан. График cos x имеет форму синусоиды и пересекает ось ординат в точке (0,1), а затем колеблется между -1 и 1, когда x изменяется на интервале от 0 до 2π.
Анализ результатов

Исследуя график функции у = cos x, можно заметить, что она представляет собой периодическую кривую, колеблющуюся между значениями -1 и 1. График симметричен относительно оси ординат, что связано с четностью функции cos x. При этом график не имеет точек разрыва, и он гладко меняет свою кривизну при переходе через точки локальных минимумов и максимумов. Также можно заметить, что период функции у = cos x составляет 2π, что подтверждает периодичность ее колебаний.
1. График функции y = cos x симметричен относительно оси ординат.
2. Период функции у cos x равен 2π и отражается в графике.
3. Ветви графика функции y = cos x лежат в интервале [-1, 1] и не имеют горизонтальных асимптот.
Исходя из проведенного анализа, рекомендуется учитывать особенности графика функции у cos x при решении задач и анализе данных.
Вопрос-ответ

Что такое график функции у cos x?
График функции y = cos x – это график, который показывает зависимость значения косинуса угла x от самого угла x. Он представляет собой плавную кривую, периодически повторяющуюся с периодом 2π и принимающую значения в интервале от -1 до 1.
Как определить, принадлежит ли график у cos x данной функции?
График у cos x принадлежит функции y = cos x, так как он является графиком значения косинуса функции. Однако, следует уточнить контекст вопроса для точного ответа.
Какие особенности имеет график функции у cos x?
График функции y = cos x обладает основной особенностью – периодичностью. Он повторяется с периодом 2π и имеет максимумы в точках (2πn, 1) и минимумы в точках (2πn + π, -1), где n – целое число. График также симметричен относительно оси ординат.
Как изучать и анализировать график функции у cos x?
Для изучения графика функции y = cos x необходимо анализировать его периодичность, точки максимумов и минимумов, симметрию и знаки значений на различных участках. Можно также использовать особенности кривой, чтобы решать уравнения и неравенства, связанные с косинусом.



