Окружность – одна из самых фундаментальных геометрических фигур, которая имеет множество интересных свойств. Одним из таких свойств является то, что хорда, соединяющая две точки окружности, лежит в одной плоскости с самой окружностью. Это утверждение может показаться очевидным, но его доказательство требует определенной логики и внимания к деталям.
Доказательство: Рассмотрим точки A и B, принадлежащие окружности, и проведем через них хорду AB. Теперь предположим, что эта хорда не лежит в плоскости окружности. Значит, существует третья точка C такая, что AC и BC не лежат на одной прямой. Однако такое предположение приводит к противоречию с свойствами окружности, в частности, с тем, что дуга AB является кратчайшим путем между точками A и B.
Примеры применения этого свойства можно найти в различных областях геометрии, начиная от построения различных фигур до решения задач на нахождение расстояний и углов. Понимание того, что хорда окружности принадлежит плоскости, помогает нам лучше понимать пространственные отношения и использовать их в практических задачах.
Доказательство отрезка на окружности
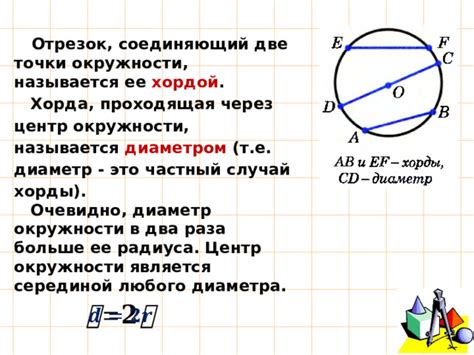
Пусть дана окружность с центром в точке O и радиусом r, а также хорда AB, принадлежащая этой окружности.
Для доказательства того, что отрезок AB лежит на окружности, можно воспользоваться следующим рассуждением:
Длина хорды AB равна расстоянию между точками A и B. По определению, окружность – это множество всех точек, равноудаленных от центра окружности. Следовательно, точки A и B, лежащие на окружности, находятся на одинаковом расстоянии от центра окружности O.
Таким образом, отрезок AB принадлежит окружности с центром в точке O и радиусом r.
Использование равнобедренного треугольника
Пусть точка P лежит на хорде окружности, и мы хотим доказать, что точка P лежит в плоскости, содержащей хорду AB.
Из свойств равнобедренного треугольника следует, что отрезок BM = CM. Посмотрим на треугольник BPM. Так как BM = CM и MP – общая сторона, то углы BMP и CMP также равны. Это означает, что точка P лежит на плоскости, содержащей хорду AB.
Применение теоремы касательной
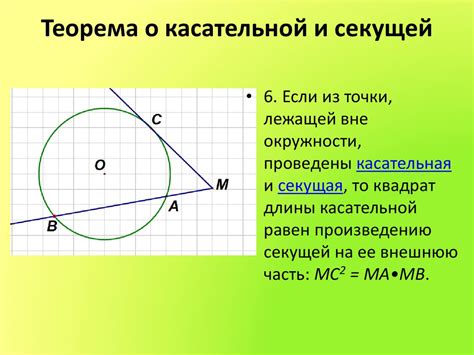
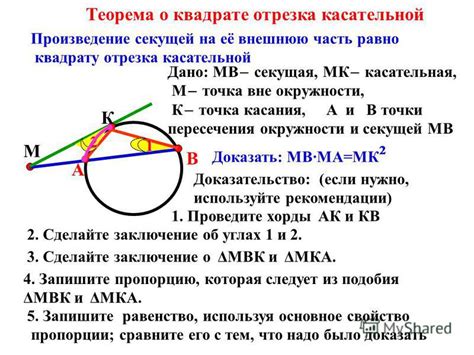
Теорема о хорде окружности также может использоваться для решения задач, связанных с касательными. Например, если из точки касания касательной с окружностью провести отрезок до центра окружности, то этот отрезок будет радиусом окружности. Это следует из того, что радиус, проведенный к центру окружности, перпендикулярен касательной, и, следовательно, образует прямой угол с ней.
Таким образом, теорема о хорде окружности может быть применена не только при работе с хордами и их длинами, но и для решения задач, связанных с касательными и радиусами окружностей.
Примеры хорд на окружности
Хорда, пересекающая диаметр
Пример: пусть дана окружность с диаметром AB и хордой CD, пересекающей диаметр в точке E. Тогда AE = EB и CE = ED, так как хорда CD делит диаметр на две равные части.
Хорда, параллельная диаметру
Например, пусть дана окружность с диаметром AB. Рассмотрим хорду CD, параллельную диаметру AB и проходящую через его середину O. Так как CD параллельна диаметру AB и проходит через его середину, то она также является диаметром окружности.
Полезные свойства хорд
1. Диаметр окружности – самая длинная хорда
Диаметр окружности является самой длинной хордой, так как он проходит через центр окружности и имеет наибольшую длину среди всех хорд данной окружности.
2. Зависимость длины хорды от расстояния от центра окружности
Для любой хорды можно сказать, что ее длина уменьшается, если она ближе к центру окружности, и увеличивается, если она дальше от центра. Это свойство позволяет легко сравнивать хорды, их длины и положение относительно центра окружности.
3. Ортогональность хорд
Если две хорды, пересекающиеся в окружности, ортогональны (перпендикулярны) друг другу, то точка пересечения этих хорд является центром окружности. Это свойство помогает определять центр окружности и строить ее геометрически.
Вопрос-ответ

Как доказать, что хорда окружности принадлежит плоскости?
Для доказательства того, что хорда окружности принадлежит плоскости, можно воспользоваться теоремой о том, что если два сегмента пересекают окружность, то их центры и точка пересечения лежат на одной прямой. Таким образом, хорда окружности представляет собой отрезок прямой, лежащий в данной плоскости.
Можете привести пример ситуации, когда хорда окружности принадлежит плоскости?
Например, если взять окружность на плоскости и провести через нее две точки, соединив их отрезком, то эта отрезок будет являться хордой окружности и лежать в той же плоскости, на которой находится окружность. Таким образом, хорда будет принадлежать плоскости, на которой они находятся.



