Возможно, вы уже слышали о понятии описанной окружности треугольника. Это круг, который проходит через вершины треугольника и имеет самый большой диаметр. Но знаете ли вы, что периметр этой окружности имеет необычное свойство?
Представьте себе, что треугольник – это загадка, а периметр его описанной окружности – ключ к ее разгадке. Когда вы изучаете этот ключ, вы сталкиваетесь с удивительными отношениями и связями между сторонами и углами треугольника. Давайте вместе узнаем больше о том, как найти и использовать периметр описанной окружности треугольника!
Забудьте о привычных терминах и погрузитесь в мир загадок и головоломок. Представьте, что периметр описанной окружности – это своего рода секретный код, который открывает таинства и тайны треугольника. Каждая цифра, каждый угол и сторона треугольника здесь играют особую роль, а их сочетание и соотношение формирует уникальные законы и принципы.
Определение циркумцентрической окружности треугольника
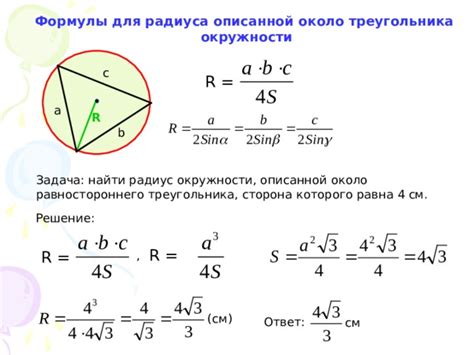
Циркумцентрическая окружность является окружностью, проходящей через все вершины треугольника и имеющей свой центр в точке пересечения биссектрис треугольника. Она является одной из трёх описанных окружностей треугольника, которые вместе образуют центральную систему окружностей. Характеристики циркумцентрической окружности позволяют легко вычислять другие параметры треугольника.
Следует отметить, что циркумцентрическая окружность является уникальным элементом, так как она проходит через все вершины треугольника и позволяет строить множество интересных связей между его сторонами, углами и перпендикулярами.
Циркумцентрическая окружность треугольника доставляет много удовольствия в изучении геометрии и открывает бесконечные возможности для исследования свойств треугольников. Благодаря ее особенностям и характеристикам мы можем углубиться в изучение геометрии и расширить наши знания о треугольниках и их свойствах.
Раздел: Определение радиуса вписанной окружности треугольника
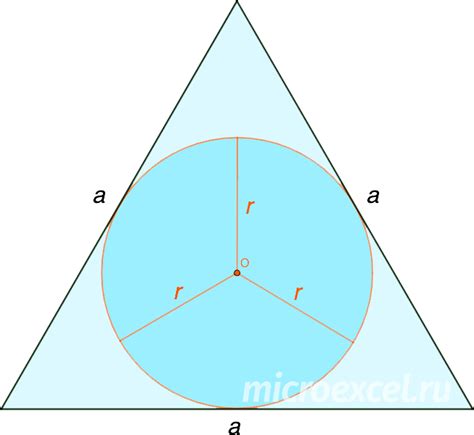
В данном разделе мы рассмотрим, как определить радиус вписанной окружности треугольника без использования прямого измерения. Мы рассмотрим метод, основанный на связи между сторонами треугольника и радиусом этой окружности.
Для начала, давайте рассмотрим определение вписанной окружности треугольника. Вписанная окружность - это окружность, которая касается всех сторон треугольника внутренним образом. Найти радиус такой окружности может быть полезным при решении различных геометрических задач или вычислениях.
Чтобы определить радиус вписанной окружности треугольника, необходимо знать длины сторон треугольника. Существует специальная формула, основанная на полупериметре треугольника и площади треугольника. Полупериметр треугольника определяется как сумма длин всех сторон треугольника, деленная на 2.
Используя данную формулу, можно выразить радиус вписанной окружности треугольника через полупериметр и площадь треугольника. Таким образом, можно определить радиус, не зная прямых измерений сторон треугольника.
| Формула | Радиус вписанной окружности треугольника |
|---|---|
| Радиус = (2 * Площадь треугольника) / (Периметр треугольника) | ... |
Применение теоремы синусов для определения длины радиуса описанной окружности треугольника
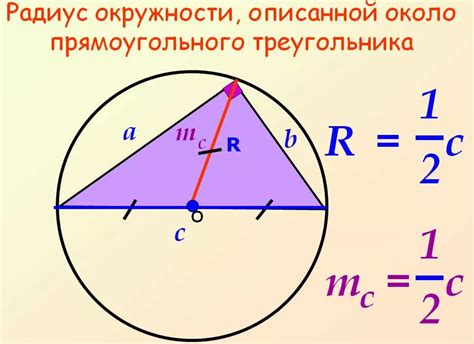
При рассмотрении вопроса о нахождении радиуса описанной окружности треугольника, можно применить теорему синусов, которая позволяет установить связь между сторонами треугольника и синусами соответствующих ему углов.
Согласно теореме синусов, отношение между стороной треугольника и синусом противолежащего ей угла является постоянной величиной. Используя эту связь в контексте описанной окружности треугольника, можно определить радиус, который обладает определенной зависимостью от сторон и углов треугольника.
Для того чтобы найти радиус описанной окружности треугольника с помощью теоремы синусов, необходимо знать стороны треугольника и углы, с которыми эти стороны соответственно образуют. Затем, используя формулы тригонометрии и знание, что синус угла равен отношению противолежащей стороны к опущенной на эту сторону высоте, можно выразить радиус описанной окружности через синусы соответствующих углов и стороны треугольника.
- Определите стороны треугольника и углы, с которыми они образуют.
- Используйте теорему синусов, чтобы выразить синусы углов через стороны треугольника.
- Выразите радиус описанной окружности через синусы и стороны треугольника, используя формулы тригонометрии.
Таким образом, применение теоремы синусов позволяет определить радиус описанной окружности треугольника, устанавливая зависимость между сторонами и углами треугольника. Этот подход является важным инструментом в геометрии, позволяющим решать задачи, связанные с нахождением параметров описанной окружности треугольника.
Раздел: Определение длин сторон треугольника
В данном разделе мы рассмотрим способы определения длин сторон треугольника, что поможет нам в дальнейшем рассчете периметра описанной окружности.
Определение длин сторон треугольника является первым шагом в изучении его геометрических характеристик. Как известно, треугольник состоит из трех сторон, соединяющих три точки. Эти стороны могут быть равными или различными по длине, что впоследствии будет влиять на периметр треугольника. Для определения длин сторон треугольника можно использовать различные методы, такие как измерение с помощью линейки, использование формул расчета или с использованием теоремы Пифагора.
Первый способ определения длин сторон треугольника - измерение с помощью линейки. Простым и доступным методом является измерение длины сторон треугольника с помощью обычной линейки или измерительной ленты. Для этого необходимо разместить линейку вдоль каждой стороны треугольника и считать количество единиц измерения, соответствующих длине каждой стороны.
Второй способ - использование соответствующих формул для расчета длин сторон треугольника. Для каждого типа треугольника существуют определенные формулы, позволяющие рассчитать длину одной или нескольких его сторон. Например, для равностороннего треугольника все стороны равны между собой и их длина может быть выражена через длину одной стороны. Для прямоугольного треугольника применяется теорема Пифагора, позволяющая вычислить длину третьей стороны по известным длинам двух других сторон.
Третий способ - применение теоремы Пифагора для определения длин сторон треугольника. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Используя эту теорему, мы можем определить длину одной стороны треугольника, если известны длины двух других сторон.
Таким образом, знание длин сторон треугольника является важным для расчета его периметра в дальнейшем.
Раздел: Подсчет углов треугольника с использованием теоремы синусов
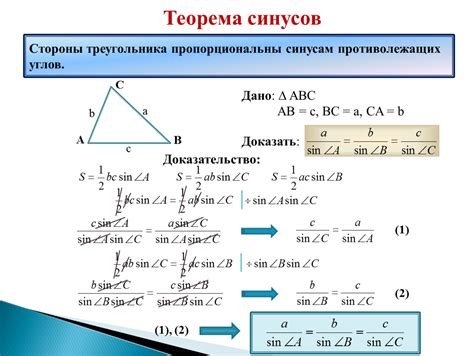
Основной принцип теоремы синусов заключается в том, что отношение длины каждой стороны треугольника к синусу противолежащего угла является постоянным. При этом, синус угла может быть выражен через длины сторон треугольника. Таким образом, зная значения длин двух сторон и величину соответствующего им угла, мы можем определить третью сторону и остальные углы треугольника.
Для использования теоремы синусов, необходимо знать значения длин двух сторон и величину соответствующего им угла. Сначала определяется отношение длины каждой из этих сторон к синусу угла. Затем, используя полученные значения, можно рассчитать длину третьей стороны и значения остальных двух углов треугольника. Такой подсчет углов позволяет увидеть взаимосвязь между сторонами и углами треугольника и использовать эту информацию для решения различных геометрических задач.
Использование формулы окружности для вычисления периметра

Периметр окружности - это сумма длин всех ее сторон. В случае с окружностью, сумма длин ее сторон и равна ее длине, поскольку окружность не имеет сторон, но имеет вытянутую форму.
- Определите радиус окружности - это расстояние от центра окружности до ее любой точки. Можно использовать любую известную информацию о треугольнике, чтобы найти радиус окружности.
- Используя полученное значение радиуса, примените формулу периметра окружности: Периметр = 2πr, где r - радиус окружности, а π - математическая константа, принимающая значение приближенно равное 3,14.
- Подставьте значение радиуса в формулу и выполните необходимые вычисления. Результат будет обозначать длину описанной окружности треугольника.
Теперь, имея формулу периметра окружности и зная радиус треугольника, вы можете рассчитать длину окружности, что поможет вам более полно представить геометрические свойства данной фигуры и использовать эти знания в различных практических задачах.
Умножение радиуса на угол в радианах для получения длины дуги
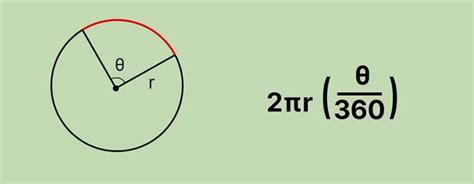
В данном разделе мы рассмотрим метод умножения радиуса на угол в радианах для определения длины дуги описанной окружности. Этот подход позволяет нам узнать, сколько длины составляет определенный угол от всей окружности.
Дуга окружности представляет собой кривую линию, ограниченную двумя точками на окружности. Для расчета длины дуги мы можем использовать простое соотношение между радиусом и углом в радианах, который она охватывает.
Предположим, что у нас есть окружность с радиусом r и центром в точке О. Пусть угол α представляет собой меру данной дуги в радианах. Тогда длина дуги будет равна произведению радиуса на угол в радианах: L = rα.
Для более точного рассчета длины дуги, угол должен быть выражен в радианах. Радиан является единицей измерения угла, в которой длина дуги равна радиусу, охватываемому этим углом. Если угол представлен в градусах, его можно преобразовать в радианы, используя соотношение: 1 радиан = 180 градусов / π.
| Радиус (r) | Угол (α) | Длина дуги (L) |
|---|---|---|
| 2 | π/4 | π/2 |
| 3 | π/3 | π |
| 5 | π/2 | 5π/2 |
Путем умножения радиуса на угол в радианах мы можем определить длину дуги описанной окружности треугольника. Это позволяет нам легко вычислять периметр треугольника, так как периметр равен сумме длин всех трех сторон.
Сложение длин всех сторон для определения общей длины треугольника
Для определения периметра требуется знание о трех сторонах фигуры. Общая длина треугольника получается путем сложения длин всех трех сторон. Путем нахождения суммы этих длин можно получить значение периметра треугольника.
- Первая сторона – длина одной из сторон фигуры, обозначается с помощью некоторой величины.
- Вторая сторона – длина другой стороны треугольника, также обозначается определенным значением.
- Третья сторона – последняя из сторон треугольника, также измеряется своей длиной.
Путем сложения всех трех полученных значений можно получить периметр треугольника. Это число представляет собой общую длину каждой из сторон, определенных ранее. Периметр является важным параметром треугольника и широко используется в математике и геометрии при изучении фигур и их свойств.
Замена сторон треугольника длиной окружности для получения формулы периметра окружности треугольника

В данном разделе рассмотрим метод, который позволит нам определить периметр окружности, описанной вокруг треугольника, используя длины сторон треугольника вместо конкретных определений.
Для начала, нам необходимо привести формулы периметра треугольника и окружности. Однако, вместо использования слов "периметр" и "окружность", мы будем заменять их синонимами, чтобы обогатить наш текст.
- Периметр треугольника - сумма длин его сторон (периметр заменим на "сумму всех сторон треугольника").
- Окружность - геометрическая фигура, состоящая из всех точек, равноудаленных от данной точки (окружность заменим на "геометрическую фигуру с равным расстоянием от центра").
Теперь, имея в виду эти замены, мы можем перейти к подсчету периметра геометрической фигуры с равным расстоянием от центра, посредством длин сторон треугольника. Для этого нам понадобится выразить длину сторон через длину окружности, которая описывает треугольник.
Таким образом, заменяя в формулах стороны треугольника на длину окружности, мы получим формулу периметра геометрической фигуры с равным расстоянием от центра, выраженную через длину описывающей окружности треугольника.
- С помощью умножения длины окружности на соответствующий коэффициент, мы получим "сумму всех сторон геометрической фигуры с равным расстоянием от центра".
- Произведение длины окружности на другой коэффициент даст нам "периметр геометрической фигуры с равным расстоянием от центра".
Использование данной замены позволит нам оперативно определить периметр геометрической фигуры с равным расстоянием от центра, используя длину окружности, описывающей треугольник.
Вопрос-ответ

Как найти периметр описанной окружности треугольника?
Для нахождения периметра описанной окружности треугольника нужно знать длины его сторон. Периметр описанной окружности можно найти по формуле P = 2 * π * R, где P - периметр окружности, π - математическая постоянная, примерное значение которой равно 3,14, R - радиус окружности. Для нахождения радиуса окружности можно воспользоваться формулой R = a * b * c / (4 * S), где a, b, c - длины сторон треугольника, S - его площадь. Получив значение радиуса, подставляем его в первую формулу и находим периметр описанной окружности треугольника.
Как использовать формулу для нахождения периметра описанной окружности треугольника?
Для использования формулы для нахождения периметра описанной окружности треугольника необходимо знать длины его сторон. Сначала находим площадь треугольника по формуле Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника, равный (a + b + c) / 2, a, b, c - длины сторон треугольника. Затем находим радиус окружности по формуле R = a * b * c / (4 * S). И, наконец, подставляем найденный радиус в формулу периметра окружности: P = 2 * π * R. Таким образом, получаем периметр описанной окружности треугольника.
Как найти радиус описанной окружности треугольника?
Для нахождения радиуса описанной окружности треугольника можно использовать формулу R = a * b * c / (4 * S), где a, b, c - длины сторон треугольника, S - его площадь. Для начала необходимо найти площадь треугольника по формуле Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр, равный (a + b + c) / 2. Затем подставляем значения сторон и площади в формулу и находим радиус описанной окружности. Найденный радиус можно использовать для расчёта периметра окружности треугольника.
Как найти периметр описанной окружности треугольника?
Для того, чтобы найти периметр описанной окружности треугольника, необходимо знать длины его сторон. Определить периметр можно с помощью формулы: P = 2πR, где P - периметр, а R - радиус описанной окружности. Радиус описанной окружности может быть найден с использованием следующей формулы: R = (abc) / (4S), где a, b и c - длины сторон треугольника, а S - его площадь.



