Изучение теории функций составляет важную часть математического курса в 10 классе. Многие из нас знакомы с понятием функции и ее основными свойствами, такими как определенность, монотонность и периодичность. Однако, на пути к более глубокому пониманию математической анализа, необходимо ознакомиться с концепцией нечетности функции.
Нечетность функции - это характеристика, отражающая ее особое поведение относительно оси симметрии. В достаточно простой форме можно сказать, что нечетная функция возвращает противоположные значения для аргументов, расположенных на разных сторонах оси симметрии. Это значит, что если значения функции для определенного аргумента положительны, то для симметричного относительно оси симметрии аргумента, функция вернет отрицательное значение и наоборот.
В данном подробном руководстве мы сосредоточимся на рассмотрении методов доказательства нечетности функции. Благодаря этой технике, мы сможем определить, является ли функция нечетной, что существенно расширяет наши возможности в анализе ее свойств. Разберемся, как использовать симметрию, алгебраические преобразования и математическую логику для построения формального доказательства.
Вводное понятие о принципе доказательства нечетности функции в школьной программе

1. Примеры функций с нечетными и четными свойствами 2. Экспериментальное наблюдение и поиск закономерностей 3. Принцип симметрии и его применение для доказательства нечетности 4. Изучение графика функции для выявления нечетности 5. Доказательство нечетности функции аналитическим методом 6. Математические операции и их влияние на свойства функции |
Теоретические основы нечетных функций
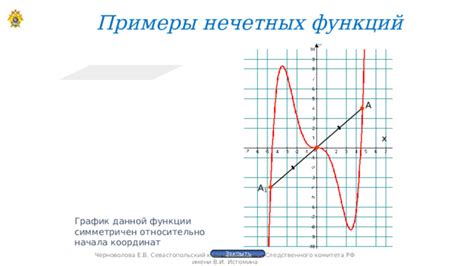
Одной из основных характеристик нечетной функции является ее симметричность относительно начала координат. Это означает, что если для функции f(x) выполняется f(x) = -f(-x), то она является нечетной. Иными словами, значение функции в точке x равно противоположному значению функции в точке -x.
Существует несколько способов доказательства нечетности функции, включая алгебраический, геометрический и аналитический подходы. Основываясь на этих методах, можно создать систему инструментов для анализа и решения задач, связанных с нечетными функциями.
Одной из интересных особенностей нечетных функций является их возможность упрощать вычисления и решение уравнений. Благодаря симметрии относительно начала координат, можно использовать свойства нечетной функции для сокращения сложности вычислений и преобразования уравнений в более простую форму.
Текущий раздел представляет собой вводный обзор теории нечетных функций. Подробнее будут рассмотрены примеры, определения и принципы доказательства нечетности функций.
Практическое применение леммы о нечетности функции

В данном разделе мы рассмотрим применение леммы о нечетности функции в реальных ситуациях. Эта лемма позволяет нам выявлять особенности поведения функции и использовать их для решения различных задач. Например, она может помочь нам определить симметричность графика функции относительно оси Oy или установить наличие или отсутствие экстремумов в заданном интервале.
Важно отметить, что практическое применение леммы о нечетности функции требует глубокого понимания самой леммы и уверенности в ее применимости для конкретной функции. Поэтому перед использованием данной леммы необходимо провести тщательный анализ функции и проверить выполнение всех необходимых условий.
| Пример | Практическое применение |
|---|---|
| Функция f(x) = x^3 | Определение симметричности графика функции относительно оси Oy |
| Функция g(x) = x^2 + 1 | Определение наличия экстремумов в заданном интервале |
| Функция h(x) = sin(x) | Исследование симметричности графика функции относительно оси Oy |
Как видно из приведенных примеров, практическое применение леммы о нечетности функции позволяет нам получить полезную информацию о самой функции и использовать ее для решения различных задач. Это очень важный инструмент для анализа и исследования поведения функций, который может быть применен в различных областях, таких как физика, экономика и другие.
Вопрос-ответ

Как доказать нечетность функции в 10 классе?
Для доказательства нечетности функции в 10 классе нужно проверить выполнение условия f(-x)=-f(x) для всех значений x из области определения функции. Если это условие выполняется, то функция является нечетной.
Какие методы можно использовать для доказательства нечетности функции?
Для доказательства нечетности функции в 10 классе можно использовать несколько методов. Один из них - это аналитический метод, который состоит в подстановке значения -x вместо x в выражение функции и проверке равенства f(-x)=-f(x). Также можно использовать графический метод, нарисовав график функции и проверив его симметричность относительно оси OY.
Какие примеры функций можно привести для доказательства нечетности функции?
Для доказательства нечетности функции в 10 классе можно привести примеры различных функций. Например, функция f(x)=x^3 является нечетной, так как f(-x)=-(-x)^3=-x^3=-f(x). Функция f(x)=sin(x) также является нечетной, так как sin(-x)=-sin(x). Такие примеры помогут лучше понять особенности нечетных функций.
Как понять, что функция, заданная графически, является нечетной?
Для понимания того, является ли функция, заданная графически, нечетной, нужно проверить симметричность графика относительно оси OY. Если график симметричен и отображает одно и то же поведение функции относительно оси OY при замене x на -x, то функция является нечетной.
Может ли функция быть одновременно и нечетной, и четной?
Нет, функция не может быть одновременно и нечетной, и четной в действительных числах. Четная функция обладает свойством f(-x)=f(x), а нечетная функция обладает свойством f(-x)=-f(x). Из этих свойств следует, что функция не может одновременно удовлетворять обоим условиям.
Как доказать нечетность функции в 10 классе?
Доказательство нечетности функции в 10 классе можно осуществить следующим образом: сначала замените аргумент функции на противоположный, затем сравните полученное значение функции с исходным. Если они разные, то функция является нечетной.



