Если вы когда-либо задавались вопросом о том, как вычислить длину всех сторон квадрата с известной его площадью, то у вас появилась возможность узнать об этом. Здесь дается простое и эффективное решение, которое поможет вам получить ответ в считанные мгновения.
Важно понимать, что периметр квадрата представляет собой сумму длин всех его сторон. Таким образом, чтобы найти периметр, необходимо знать значения всех сторон квадрата. Однако, если у вас нет этой информации, а имеется только площадь, то этот метод идеально подходит для вас.
Суть метода заключается в использовании связи между площадью квадрата и его стороной. Если вы знакомы с формулой для нахождения площади квадрата (S = a^2, где a - длина стороны), то вам будет несложно применить обратное вычисление для нахождения длины сторон.
Определение длины стороны квадрата исходя из его площади

Раздел "Определение длины стороны квадрата исходя из его площади" представляет метод, позволяющий узнать длину стороны квадрата на основе известного значения его площади. Этот способ позволяет без предварительного знания других параметров квадрата определить его геометрические характеристики и расчетные значения.
В данном разделе будут рассмотрены подходы, основанные на математических и геометрических принципах, а также числовых методах. С помощью простых формул и уравнений, мы сможем установить связь между площадью и периметром квадрата, что позволит определить длину его стороны. Благодаря этому подходу, вы сможете расчитывать периметр квадрата, даже если изначально известна только его площадь.
Основные принципы расчёта окружности квадрата
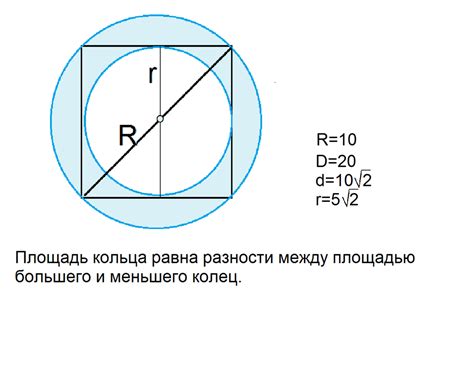
В данном разделе мы рассмотрим основные принципы, которые позволяют вычислить длину окружности квадрата. Для достижения этой цели мы опишем основные аспекты, связанные с расчётом периметра данной геометрической фигуры.
Периметр квадрата - это сумма его четырёх сторон. Для его вычисления можно использовать различные подходы и формулы, основывающиеся на площади квадрата или его диагонали. Как и в случае с площадью, применяются такие понятия, как длина стороны, диагональ и радиус вписанной окружности.
Основной принцип вычисления периметра квадрата заключается в умножении длины его стороны на 4. Это связано с тем, что квадрат имеет четыре стороны равной длины. Для определения длины стороны можем использовать различные методы, например, вычисление корня из площади квадрата или диагонали.
Кроме того, существуют и другие методы расчёта периметра квадрата, связанные с его вписанной окружностью или диагональю. Для применения этих методов требуется предварительное вычисление соответствующих значений, которые затем используются в формулах.
Важная формула для расчета окружности, основанная на площади
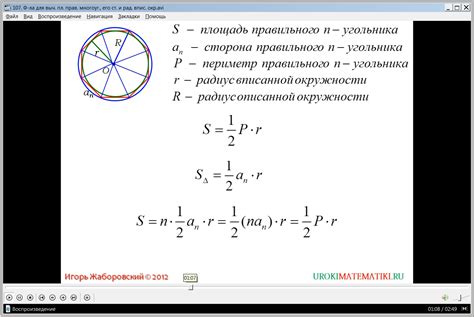
Известно ли вам, что существует эффективный способ вычисления длины окружности по ее площади?
Давайте рассмотрим простую формулу, позволяющую нам выяснить, сколько всего расстояния пересекает окружностное пятно на ее окружности. Этот метод eliminiert необходимость знать радиус окружности, фокусируясь на площади.
Один из способов вычисления окружности основан на том, что площадь окружности увязывается в тесную ассоциацию с ее окружностью. Таким образом, мы можем использовать эту связь для выведения простой формулы, не требующей знания других параметров.
Рассмотрим ситуацию, когда имеется информация только о площади окружности. Это может быть результатом маркировки на поверхности, измерения площади определенного фрагмента или просто известная величина в задаче.
Эффективной формулой расчета длины окружности, исходя из площади, является отношение площади к квадрату радиуса окружности. Если мы обратим это отношение и найдем его квадратный корень, полученное значение будет измеряться в единицах длины.
Практические примеры расчета окружности квадрата по площади
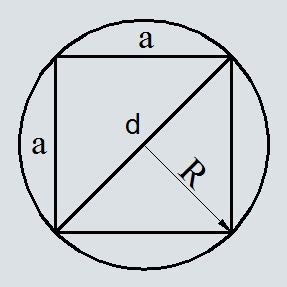
Расчет периметра квадрата по его площади часто встает перед нами в различных ситуациях. Но как выполнить этот расчет без особых хлопот и затрат времени? Давайте рассмотрим несколько практических примеров, которые помогут вам справиться с этой задачей быстро и легко.
Пример 1:
Предположим, у нас есть квадрат со стороной, известной нам как "а". Площадь этого квадрата можно выразить следующей формулой: S = a2. Для рассчета периметра по площади, нам нужно найти значение стороны "а". Используя формулу площади квадрата, мы можем найти линейные размеры этой фигуры.
Пример 2:
Допустим, у нас имеется квадрат площадью S. Если у нас есть значение площади, мы можем использовать обратную операцию возведения в квадрат, чтобы найти сторону квадрата. Найдя значение стороны, мы сможем легко найти периметр нашей фигуры.
Пример 3:
В некоторых случаях, может быть удобнее использовать готовые таблицы или программы для вычисления периметра по заданной площади. В таких решениях обычно применяются специальные алгоритмы, которые быстро и точно выполняют данную задачу.
Используя эти практические примеры, вы сможете легко и быстро рассчитать периметр квадрата по его площади, не затрачивая много времени и усилий.
Вопрос-ответ

Как вычислить периметр квадрата по его площади?
Для вычисления периметра квадрата по его площади нужно использовать формулу: P = 4 * квадратный корень из S, где P - периметр, S - площадь квадрата. Этот метод основан на простом и легко запоминающемся соотношении между периметром и площадью квадрата.
Какие данные нужны для вычисления периметра квадрата?
Для вычисления периметра квадрата по его площади необходимо знать только площадь квадрата. Другие стороны или углы квадрата не требуются, так как периметр зависит только от площади.
Как применить формулу для вычисления периметра квадрата?
Для применения формулы для вычисления периметра квадрата необходимо взять значение площади квадрата и подставить его в формулу P = 4 * квадратный корень из S, где P - периметр, а S - площадь квадрата. Затем следует вычислить квадратный корень из площади и умножить полученное значение на 4. Таким образом, вы получите значение периметра квадрата.
Какая формула используется для вычисления периметра квадрата по его площади?
Для вычисления периметра квадрата по его площади используется следующая формула: P = 4 * квадратный корень из S, где P - периметр, а S - площадь квадрата. Эта формула легка для запоминания и применения, поскольку основана на простом соотношении между периметром и площадью квадрата.



