Диагонали квадрата - это его отрезки, соединяющие противоположные вершины. Проверка на пересечение диагоналей является важным шагом при решении многих геометрических задач. В данной статье мы рассмотрим, как определить, пересекаются ли диагонали в заданном квадрате.
Квадрат - это четырехугольник, у которого все стороны равны между собой, а углы прямые. Для любого квадрата сумма его углов равна 360 градусов. Из этого следует, что диагонали квадрата равны между собой и перпендикулярны друг другу.
Проверка пересечения диагоналей
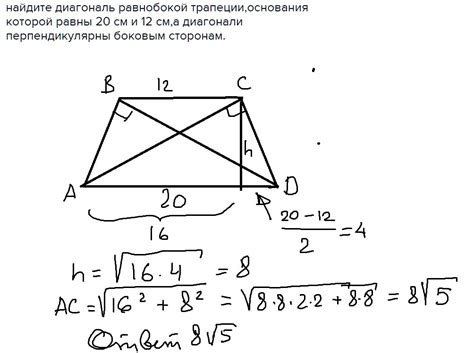
Для проверки пересечения диагоналей квадрата нужно измерить их длины. Если длины диагоналей равны, то диагонали точно пересекаются в центре квадрата. Для вычисления длины диагонали просто умножьте длину стороны квадрата на √2 (корень из 2).
| Формула для вычисления длины диагонали: | длина диагонали = длина стороны * √2 |
Метод 1: Геометрическое решение
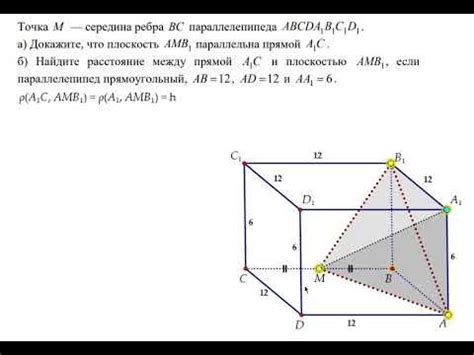
Для того чтобы определить, пересекаются ли диагонали квадрата, можно использовать геометрический метод. Давайте предположим, что у нас есть квадрат ABCD с диагоналями AC и BD. Если диагонали пересекаются, то точка их пересечения будет точкой пересечения серединных перпендикуляров к сторонам квадрата.
Для того чтобы подтвердить пересечение диагоналей, построим серединные перпендикуляры к сторонам квадрата. Затем найдем точку их пересечения, если она совпадает с центром квадрата, то диагонали пересекаются.
| Метод: | Геометрическое решение |
| Предположение: | Предположим, что диагонали пересекаются |
| Действие: | Построение серединных перпендикуляров и поиск их пересечения |
| Результат: | Если точка пересечения совпадает с центром квадрата, диагонали пересекаются |
Метод 2: Алгебраическое доказательство

Сначала найдем уравнения прямых, на которых лежат диагонали квадрата. Диагонали квадрата идут от вершины A до противоположной вершины C, и от вершины B до противоположной вершины D. Уравнение прямой, проходящей через две точки с координатами (x₁, y₁) и (x₂, y₂), можно найти по формуле: y - y₁ = (y₂ - y₁)/(x₂ - x₁) * (x - x₁).
Для диагонали AC у нас есть две точки (0,0) и (a,a). Подставим их координаты в уравнение прямой и получим уравнение диагонали AC: y = x.
Для диагонали BD у нас есть две точки (a,0) и (0,a). Подставим их координаты в уравнение прямой и получим уравнение диагонали BD: y = -x + a.
Затем найдем точку пересечения диагоналей. Для этого приравняем уравнения диагоналей и решим уравнение y = x и y = -x + a. Получим: x = a/2, y = a/2. Это точка пересечения диагоналей квадрата.
Таким образом, алгебраическое доказательство показывает, что диагонали квадрата пересекаются в его центре.
Вопрос-ответ

Как проверить пересекаются ли диагонали квадрата?
Диагонали квадрата пересекаются всегда. Для проверки этого свойства можно взять любой квадрат и нарисовать его диагонали. Вы увидите, что они точно пересекаются в одной точке, образуя прямой угол.
Почему диагонали квадрата пересекаются?
Диагонали квадрата пересекаются потому, что они делят квадрат на два равных треугольника. Эти треугольники равны по сторонам и углам, поэтому их диагонали также равны и пересекаются в одной точке.
Какие свойства имеют диагонали квадрата?
Диагонали квадрата равны по длине и пересекаются в одной точке, образуя прямой угол. Это следует из равенства сторон и углов квадрата, а также из того, что диагональ делит квадрат на два равных треугольника.
Что происходит, если диагонали квадрата не пересекаются?
Если диагонали квадрата не пересекаются, то это означает, что данная фигура не является квадратом. Проверьте правильность построения и соответствие всех сторон и углов квадрата.
Какая теорема гарантирует пересечение диагоналей квадрата?
Пересечение диагоналей квадрата следует из теоремы о пересечении диагоналей в параллелограмме, которая гласит, что диагонали параллелограмма делятся пополам и пересекаются в одной точке. Квадрат является частным случаем параллелограмма, поэтому диагонали квадрата всегда пересекаются.



