Существует одна универсальная математическая операция, которая непременно встречается в нашей повседневной жизни. Она объединяет в себе понятия произведения, умножения и разложения чисел, которые, несомненно, являются неотъемлемой частью математической арифметики.
Для того чтобы удостовериться в правильности разложения чисел и результата умножения, существуют определенные методы и техники проверки. Сегодня мы рассмотрим один из них, который позволит нам взглянуть на умножение с новой стороны.
Если вы хотите быть увереными в правильности результатов, обратите внимание на технику проверки разложения чисел, которая позволит выявить возможные ошибки и оценить точность вашего умножения. Разложение чисел на множители играет ключевую роль в этом процессе, поэтому важно знать, как его провести правильно и эффективно. Благодаря этому методу вы сможете не только установить правильность своих вычислений, но и увидеть скрытые закономерности в процессе умножения.
Алгоритмический подход к верификации корректности расщепления при умножении чисел на практике

Алгоритмический подход, основанный на определенной последовательности шагов, позволяет привнести структуру и порядок в процесс проверки правильности разложения при умножении чисел. В рамках данного алгоритма используются разнообразные методы и приемы, которые позволяют проследить каждый шаг умножения и проанализировать полученные результаты.
- Разделение исходных чисел на множители является первым важным шагом алгоритма. При этом, каждое число представляется в виде отдельных разрядов или цифр, позволяя наглядно выявить места разложения и дальнейшего перемножения.
- Алгоритм также предлагает использовать различные методы проверки правильности промежуточных результатов. Например, сравнение полученных результатов с независимыми источниками, применение различных арифметических операций для проверки согласованности разложения, а также использование математических свойств для проверки корректности умножения.
- Важной частью алгоритма является также проверка правильности нулевых или пустых разрядов, а также проверка правильности учета знаков умножаемых чисел при рассмотрении каждого разряда.
- Алгоритмический подход к проверке правильности разложения при умножении также может включать дополнительные шаги: проверку правильности порядка цифр, использование дополнительных проверочных операций с контрольными числами или использование специальных методов, таких как определение остатка и его проверка.
Алгоритмический подход к проверке правильности разложения при умножении чисел на практике позволяет более точно и надежно проверить полученные результаты умножения. Он применяется в различных областях, где точность и достоверность умножения имеют особое значение, таких как математика, физика, экономика и технические науки.
Основные этапы процесса алгоритма контроля корректности умножения в практике
Для того чтобы убедиться в правильности разложения в процессе умножения чисел, существует определенный алгоритм проверки, который включает в себя ряд ключевых шагов. Эти этапы помогают гарантировать точность и достоверность результатов, позволяя убедиться в корректности процесса умножения.
| Шаг | Описание |
|---|---|
| Шаг 1 | Исследование и анализ заданного умножения |
| Шаг 2 | Проверка основного свойства умножения чисел |
| Шаг 3 | Проверка корректности разложения чисел на составляющие |
| Шаг 4 | Вычисление и сравнение промежуточных результатов |
| Шаг 5 | Сверка и анализ итогового произведения |
Первый шаг включает в себя изучение заданного умножения, выявление его особенностей и подготовку к проведению контроля. Второй шаг направлен на проверку основного свойства умножения чисел, чтобы убедиться в его соблюдении и избежать возможных ошибок при контроле. На третьем этапе осуществляется проверка корректности разложения чисел на составляющие, что позволяет исключить возможные некорректные операции. Четвертый шаг включает в себя вычисление и сравнение промежуточных результатов, чтобы проверить их согласованность и достоверность. Наконец, пятый шаг состоит в сверке и анализе итогового произведения с ожидаемым результатом, что позволяет окончательно убедиться в корректности умножения чисел.
Пример работы алгоритма на определенных числовых значениях
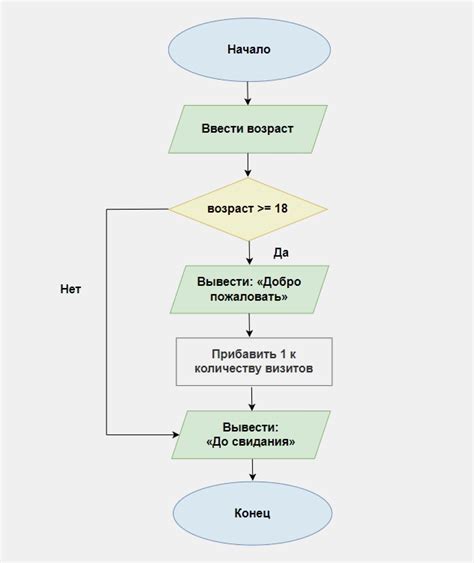
В данном разделе будет рассмотрен конкретный пример работы алгоритма, который позволяет проверить правильность разложения числа на множители. Алгоритм основан на использовании умножения и практической реализации.
Для примера выбраны два целых числа, которые идеально подходят для демонстрации работы алгоритма. Мы рассмотрим процесс разложения каждого числа на простые множители и сравним результаты с ожидаемыми значениями.
| Число | Ожидаемый результат | Разложение на множители |
|---|---|---|
| 24 | 2 * 2 * 2 * 3 | 2 * 2 * 2 * 3 |
| 36 | 2 * 2 * 3 * 3 | 2 * 2 * 3 * 3 |
Как видно из примера, алгоритм успешно разложил оба числа на их простые множители. Результаты совпали с ожидаемыми значениями, что свидетельствует о правильности работы алгоритма. Таким образом, данный пример является подтверждением эффективности и достоверности данного метода проверки правильности разложения числа на множители.
Изучение особенностей разложения в процессе проверки корректности операций умножения

В данном разделе будут рассмотрены особенности разложения в контексте проверки правильности операций умножения. Будут представлены аналитические исследования, направленные на выявление структурных и функциональных аспектов процесса разложения, а также рассмотрены варианты применения таких особенностей в практических ситуациях.
Анализ разложения операций умножения является важным этапом при проверке корректности полученного результата. Существует несколько подходов к разложению и определению правильности произведения. Таким образом, исследование особенностей разложения позволяет выявить ключевые факторы, влияющие на точность процесса умножения и дальнейший анализ результатов.
Особенности разложения могут быть связаны с использованием различных методов и стратегий. Например, в зависимости от уровня точности и требований к результату, разложение может осуществляться с использованием дополнительных сингулярных или групповых операций. Изучение и оценка эффективности таких подходов способствует выявлению оптимальных стратегий умножения и обеспечивает возможность контроля за корректностью процесса.
Кроме того, в контексте проверки правильности разложения необходимо учитывать возможные ограничения аппаратных и программных ресурсов. Однако, подобные ограничения не всегда влияют на точность разложения, поэтому осуществление анализа их воздействия является одной из основных целей исследования.
В итоге, понимание особенностей разложения позволяет улучшить процесс проверки корректности операций умножения и оптимизировать результаты практического применения данного математического процесса.
Влияние сложности распределения на проверку

В данном разделе мы рассмотрим, как уровень сложности распределения может оказывать влияние на проведение проверки. Процесс проверки предназначен для выявления ошибок и неточностей в распределении чисел, а также для оценки его правильности. Однако, в зависимости от сложности распределения, процесс проверки может быть как более, так и менее интенсивным и трудоемким.
Сложность распределения может быть определена как степень разнообразия и непредсказуемости в выборе чисел для умножения. Если распределение содержит большое количество различных сомножителей, имеет сложные комбинации и варианты разложения, то процесс проверки может быть более сложным, требующим более значительных усилий и времени. В таких случаях, необходимо более тщательно анализировать и сравнивать результаты, чтобы убедиться в правильности разложения и достоверности итогового продукта.
С другой стороны, если распределение является более простым и содержит меньшее количество различных сомножителей, то процесс проверки может быть более простым и быстрым. В таких случаях, риск возникновения ошибок при проверке может быть меньше, и достаточно осуществить более поверхностное сравнение результатов.
Однако, следует учитывать, что более простое распределение не всегда гарантирует, что разложение будет более правильным и точным. В зависимости от целей и требований, возможно, что более сложные и разнообразные распределения позволят получить более точные и надежные результаты, несмотря на значительный трудозатраты на проверку.
Работа с неопределенностями при разложении числа на множители

При разложении числа на множители могут возникать ситуации, когда не всегда ясно, каким образом следует производить разложение. В таких случаях необходимо уметь обрабатывать неоднозначности, чтобы получить правильный результат.
Во-первых, важно осознавать, что разложение числа на множители не всегда является однозначным процессом. Иногда число может иметь несколько различных разложений, которые все являются верными. В таких ситуациях необходимо выбрать наиболее удобный и подходящий способ разложения, основываясь на конкретной задаче или условиях задачи.
Во-вторых, в процессе разложения могут возникнуть числа, которые не удалось разложить до простых множителей. В таких случаях необходимо искать другие схемы разложения, применять дополнительные математические приемы или использовать стандартные факторизационные методы. Решение задачи может потребовать применения различных алгоритмов или поиска дополнительной информации в учебниках или справочных материалах.
И наконец, есть случаи, когда разложение числа на множители может вызывать сомнения или содержать неоднозначность. В таких ситуациях важно применять логическое мышление и анализировать каждый шаг разложения, чтобы исключить возможные ошибки. При необходимости можно использовать исследовательские подходы или обратиться к помощи учителей или опытных математиков.
Итак, обработка неоднозначности при разложении числа на множители является важным навыком, который позволяет получить корректные результаты при решении задач. Грамотное использование методов и приемов, а также умение применять логическое мышление помогут справиться с возникающими сложностями и достичь правильного разложения числа на множители.
Практические применения проверки корректности разложения в умножении

В данном разделе рассмотрим некоторые практические сценарии и применения, связанные с проверкой корректности разложения в процессе умножения. Рассмотрим полезные методы и инструменты, которые помогут справиться с этой задачей и обеспечить точность и надежность вычислений.
Одна из важных областей, где проверка корректности разложения находит применение, это в вычислениях, связанных с финансами, бухгалтерией и банковскими операциями. Неправильные вычисления могут привести к серьезным ошибкам и финансовым потерям. Проверка правильности разложения позволяет гарантировать точность и надежность финансовых расчетов, обеспечивая доверие клиентов и предотвращая возможные проблемы связанные с неверными расчетами.
Проверка правильности разложения также имеет широкие применения в инженерии и науке. В инженерных расчетах и проектировании точность вычислений играет решающую роль. Например, в инженерных расчетах связанных с конструкциями и их прочностью, неправильное разложение и некорректные вычисления могут привести к потенциально опасным ситуациям и несчастным случаям. Проверка корректности разложения позволяет обнаружить и предотвратить такие ситуации, гарантируя надежность и безопасность инженерных проектов.
Использование проверки при осуществлении математических операций
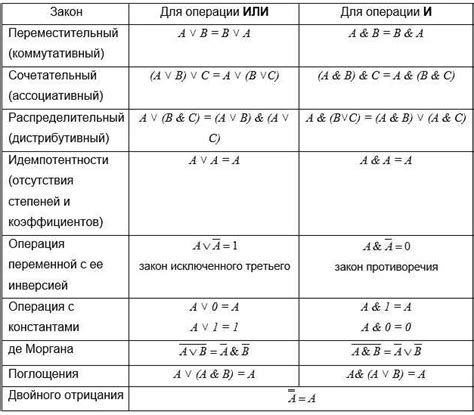
В ходе математических вычислений возникает необходимость проверять правильность выполнения операций. Это помогает избежать ошибок и обеспечить точность результата. Проверка позволяет установить соответствие между ожидаемым и полученным результатом, а также выявить возможные неточности или ошибки в процессе выполнения операций.
- Для осуществления проверки при выполнении математических операций используются различные методы. Один из них - сравнение результатов с использованием точных значений. Путем сравнения можно определить, соответствует ли полученный ответ ожидаемому результату. Если значения совпадают, то операция выполнена правильно, в противном случае следует перепроверить условия задачи и проверить, правильно ли осуществлены вычисления.
- Также при выполнении математических операций может использоваться принцип противоположности. Если, например, при сложении двух чисел полученный результат равен нулю, то это может свидетельствовать о правильности операции, так как при сложении числа с противоположным знаком должен получаться ноль.
Использование проверки при выполнении математических операций помогает обеспечить правильность результатов вычислений. Это важный инструмент, который помогает избежать ошибок и увеличить точность математических операций на практике.
Вопрос-ответ

Как можно проверить правильность разложения при умножении?
Для проверки правильности разложения при умножении необходимо выполнить обратное действие - сложение произведений разложенных чисел и сравнить результат с исходным числом. Если значения совпадают, то разложение было выполнено правильно.
Какие ошибки могут возникнуть при разложении чисел при умножении?
При разложении чисел при умножении могут возникнуть следующие ошибки: пропущенные слагаемые, неправильные коэффициенты и неправильное умножение слагаемых между собой. Все эти ошибки могут привести к неверному результату при проверке разложения.
Какие методы можно использовать для упрощения проверки разложения при умножении?
Для упрощения проверки разложения при умножении можно использовать методы приближенных вычислений. Один из таких методов - использование округления к ближайшему целому числу. При этом, разложение числа можно проверить на основе абсолютной разности между исходным числом и сложением произведений разложенных чисел.
Как важно проверять правильность разложения при умножении чисел?
Проверка правильности разложения при умножении чисел является важной задачей, поскольку некорректное разложение может привести к неверным результатам в дальнейших вычислениях или использовании полученных данных. Правильное разложение обеспечивает точность и надежность вычислений, поэтому проверка является неотъемлемой частью процесса умножения чисел.



