Всем нам знакомы числа и арифметические операции, но редко задумываемся над их внутренней структурой и правилами, которые определяют их взаимосвязь. Одним из таких правил является деление на 7.
Деление на 7 – это операция, которая позволяет нам разделить одно число на другое и получить остаток. Но зачем это нужно и какие существуют правила для такого деления? Рассмотрим это подробнее.
Расчет делимого с делителем 7 является неотъемлемой частью математики и находит свое применение в различных областях науки и повседневной жизни. Он позволяет нам анализировать и обрабатывать данные, находить закономерности и решать сложные задачи.
Что такое делимое и делитель в математике

Делимое – это число, которое мы делим на другое число, называемое делителем. Причем, приделении делимого на делитель, мы ожидаем получить результат, называемый частным. В свою очередь, в математике существуют различные правила и методы, которые позволяют нам рассчитать частное числа, разделив его на делитель.
Для лучшего понимания, представим ситуацию, когда у нас есть некоторое количество предметов, которое мы хотим поделить на одинаковые группы. Это количество предметов будет нашим делимым числом, в то время как количество групп будет являться делителем. Делимое и делитель тесно связаны друг с другом и позволяют нам проводить вычисления и решать разнообразные задачи.
Основные понятия в расчете делимого на делитель 7

В данном разделе мы рассмотрим важные термины и понятия, связанные с процессом расчета делимого на делитель 7. Понимание этих терминов поможет нам более глубоко вникнуть в суть и принципы этой математической операции.
- Делимое: числовое значение, которое мы делим на делитель. В данном случае, речь идет о делимом, кратном 7.
- Делитель: число, на которое мы делим делимое. В нашем случае делитель всегда равен 7.
- Деление нацело: процесс расчета, в результате которого делимое делится на делитель без остатка. Если результат деления нацело равен целому числу, то говорят, что делимое является кратным делителю.
- Остаток: число, которое остается после выполнения деления. Если при делении делимого на делитель получается остаток, то можно сказать, что делимое не является кратным делителю.
Эти основные понятия являются ключевыми для понимания принципов и правил расчета делимого на делитель 7. Далее мы рассмотрим конкретные примеры, чтобы наглядно продемонстрировать, как эти понятия применяются на практике.
Практические методы для расчета чисел, делящихся на 7

В этом разделе мы рассмотрим несколько удобных способов для определения чисел, которые делятся на 7 без остатка. Знание этих правил поможет вам быстро и точно выполнять подобные вычисления в уме.
- Одним из методов является основанное на повторении последовательности чисел семейное правило. Согласно ему, если к числу последовательно прибавить или вычесть 7 несколько раз, и результат каждого шага также будет делиться на 7, то и исходное число также будет делиться на 7. Это правило позволяет быстро и легко определить, можно ли разделить число на 7 без остатка.
- Альтернативным методом является использование перестановки разрядов числа. Если цифры числа переставить в другом порядке, то полученное число будет делиться на 7, если исходное число также делилось на 7. Этот способ особенно полезен при работе с длинными числами, где перестановка разрядов более эффективна, чем применение арифметических операций.
- Некоторые числа при делении на 7 могут оставлять остаток, но этот остаток также подчиняется специальным правилам. Например, если остаток от деления числа на 7 равен 1, то результатом деления "число - остаток" также будет делиться на 7. Аналогично, если остаток от деления равен 2, 3, 4, 5 или 6, то результатом деления "число + (7 - остаток)" также будет делиться на 7.
Использование этих правил позволяет легко и безошибочно определить, делится ли число на 7 без остатка, без необходимости выполнять само деление. Изучив эти методы и потренировавшись в их применении, вы сможете быстро и точно расчитывать числа, которые делятся на 7.
Как узнать, кратно ли число 7

Когда мы имеем дело с большими числами, вычисление деления на 7 может показаться сложной задачей. Однако существуют определенные правила и методы, позволяющие быстро определить, делится ли число на 7 без использования калькулятора.
Для начала, мы можем использовать процесс последовательного вычитания чисел, кратных 7. Если в результате вычитания число станет кратным 7, то исходное число также будет кратным 7. Например, если мы вычитаем 21 из числа и получаем 42, то исходное число 63 делится на 7.
Другой метод - проверка правила делимости на 7. Если сумма цифр числа минус удвоенная последняя цифра делится на 7, то исходное число также делится на 7. Например, для числа 168, давайте выполним следующие шаги: сумма цифр (1+6+8=15) минус удвоенная последняя цифра (8*2=16). Результат равен -1. Так как -1 не делится на 7, число 168 не делится на 7.
Таким образом, расчет деления на 7 не так сложен, как может показаться на первый взгляд. Используя эти простые методы, мы можем быстро определить, делится ли число на 7 и избежать сложных вычислений.
Как определить остаток от деления числа на 7
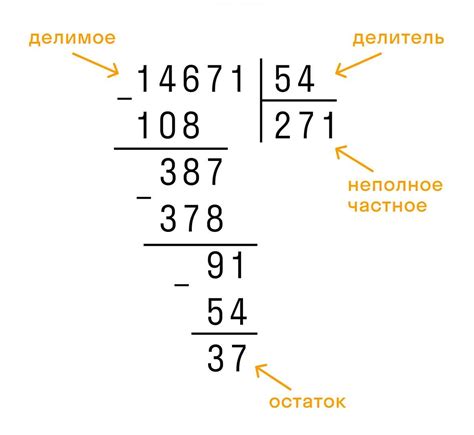
Существует несколько простых способов определения остатка от деления числа на 7. Один из них основан на использовании периодичности чисел при делении на 7. Если число делится на 7 без остатка, то его остаток будет равен 0. Если после деления получается остаток 1, то его можно интерпретировать как число, сдвинутое вправо на одну единицу. Остаток 2 соответствует сдвигу числа на две единицы и так далее. Если после деления числа на 7 получается остаток 6, то можно сказать, что число сдвинуто влево на одну единицу.
Другой способ определения остатка от деления на 7 связан с использованием суммы цифр числа. Для этого нужно сложить все цифры числа, затем вычесть из полученной суммы удвоенную сумму цифр числа, образованного последними тремя цифрами числа, и повторять эту операцию до тех пор, пока не будет получен однозначный результат. Если этот результат равен 0, то исходное число делится на 7 без остатка. Если результат равен 1, то остаток от деления на 7 будет 1, и так далее.
Определение остатка от деления числа на 7 является одним из базовых правил в математике и может быть использовано для решения различных задач. Понимание этих правил и их практическое применение помогут вам более эффективно работать с числами в повседневной жизни и в учебе.
Метод вычисления чисел, делящихся на 7, с примерами

В данном разделе мы рассмотрим уникальный метод, позволяющий определить числа, которые делятся на 7. Этот метод основан на специфических правилах, которые позволяют нам вывести ряд чисел, обладающих данной особенностью. Ниже приведены примеры, которые помогут наглядно понять принцип этого метода.
| Делимое | Результат |
|---|---|
| 7 | 1 |
| 14 | 2 |
| 21 | 3 |
| 28 | 4 |
| 35 | 5 |
Как видно из примеров, чтобы определить результат деления числа на 7, достаточно взять последнюю цифру этого числа и, при необходимости, повторять процесс до тех пор, пока не получим однозначное число. Такой подход позволяет легко и оперативно вычислить результат деления на 7 для любого числа.
Шаги метода для вычисления результатов при делении на число 7: детальное объяснение

В этом разделе представлено подробное объяснение шагов метода, которые позволят вам правильно рассчитать результаты при делении любого числа на число 7.
1. Шаг первый – анализ цифр числа: для начала необходимо внимательно изучить цифры, из которых состоит наше число, и по возможности разложить их на составные части. Здесь может пригодиться знание синонимов.
2. Шаг второй – проверка на делимость: важно определить, делится ли число на 7 без остатка. Для этого нужно просуммировать числа, составляющие данное число, и проверить, делится ли получившаяся сумма на 7.
3. Шаг третий – вычисление остатка: если число не делится на 7 без остатка, то остаток нужно вычислить и запомнить его. Это можно сделать, вычитая из суммы чисел остаток, полученный после деления суммы на 7.
4. Шаг четвертый – деление на делимое: после вычисления остатка, необходимо разделить полученную сумму на 7, чтобы получить результат деления на число 7.
5. Шаг пятый – проверка корректности результата: важно проверить, является ли полученный результат правильным, используя различные методы проверки, например, проверку умножением на делитель и складыванием с остатком.
Понимание и применение этих шагов помогут вам легко и точно рассчитывать результаты при делении любого числа на 7, используя простые и понятные методы.
Примеры использования метода деления на 7

В данном разделе мы рассмотрим практические примеры, демонстрирующие применение метода деления на 7 для расчета различных чисел. Этот метод основан на простых математических законах и позволяет легко и точно определить, делится ли число без остатка на 7.
Представим, что у нас есть число, и мы хотим определить, делится ли оно на 7. Сначала мы делим это число на 7, а затем анализируем полученное частное и остаток. Если остаток равен нулю, то число делится на 7 без остатка, если остаток не равен нулю, то число не делится.
Для лучшего понимания метода, рассмотрим несколько примеров. Например, возьмем число 56. Разделим его на 7: 56 ÷ 7 = 8. В данном случае полученное частное равно 8, а остаток равен 0, что означает, что число 56 делится на 7 без остатка.
Теперь рассмотрим другой пример. Возьмем число 43. Разделим его на 7: 43 ÷ 7 = 6. При данном делении получаем частное равное 6, а остаток равен 1. Из этого следует, что число 43 не делится на 7 без остатка.
Как видно из данных примеров, метод деления на 7 позволяет нам легко определить, делится ли число на 7. Этот метод может быть полезен при решении различных математических и практических задач, связанных с делением и долей.
Альтернативные способы вычисления чисел, кратных 7
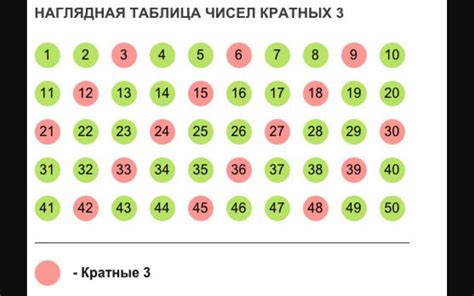
1. Метод "семерок"
В первом методе мы будем разбивать исходное число на группы из трех цифр, начиная с конца числа. Затем будем складывать полученные группы и проверять, делится ли полученная сумма на 7. Если делится, то исходное число также кратно 7. Например, для числа 1234567 мы разобьем его на группы 1-234-567 и получим сумму 1 + 234 + 567 = 802, которая делится на 7 без остатка. Следовательно, число 1234567 является кратным 7.
2. Метод "уравнений"
Второй метод основан на использовании уравнений. Мы будем рассматривать число, умноженное на 10, и затем вычитать из этого числа само число. Если результат делится на 7 без остатка, то исходное число также кратно 7. Например, для числа 42 мы выполняем следующие действия: 42 * 10 = 420, затем 420 - 42 = 378. Полученное число 378 делится на 7 без остатка, следовательно, число 42 является кратным 7.
3. Метод "факторизации"
Третий метод основан на простой факторизации числа и степенях числа 10. Мы будем искать степень числа 10, при которой полученное число делится на 7 без остатка. Например, для числа 189 мы будем проверять, делится ли 189 на 10 в степени 1, 10 в степени 2, и т.д. Поскольку 189 не делится на 7 без остатка при любой степени числа 10, это число не является кратным 7.
Использование этих альтернативных методов позволяет нам расширить наше понимание и навыки в области математики. Вы можете использовать их для увлекательного размышления и развития интуиции в решении математических задач.
Использование таблицы умножения для быстрого и эффективного расчета
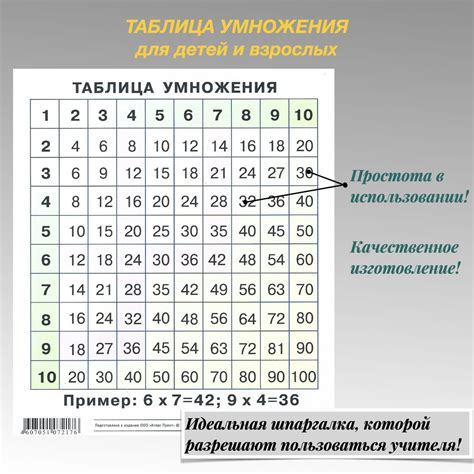
Отличный способ быстро и точно рассчитать делимое, используя таблицу умножения, которая содержит все необходимые множители. Это универсальный инструмент, который поможет вам сократить время и сделать расчеты более легкими и понятными.
Каждое число в таблице умножения представлено в четырех разных категориях, а именно: числа, которые кратны семи; числа, которые можно поделить на семь нацело; числа, которые не являются кратными и не могут быть поделены на семь; и числа, которые являются остатками от деления на семь.
Для быстрого расчета делимого с делителем 7, просто найдите в таблице умножения нужное число и определите его категорию. Например, если вы хотите найти делимое числа 14, найдите число 2 в категории "числа, которые можно поделить на семь нацело". Затем умножьте это число на 7 и получите нужный результат - 14.
Таким образом, использование таблицы умножения позволяет быстро и точно определить делимое с делителем 7 без необходимости проводить сложные вычисления. Это простой и эффективный способ осуществлять подобные расчеты, что особенно полезно при работе с большими числами или при необходимости быстрого решения задач.
Применение упрощенных алгоритмов при делении на 7
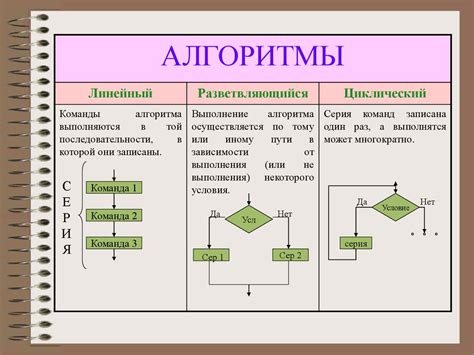
В данном разделе мы рассмотрим некоторые методы и правила, которые помогут нам производить деление на 7 с минимальными усилиями и высокой точностью. Эти упрощенные алгоритмы представляют собой действия, с помощью которых можно быстро и эффективно определить, делится ли число на 7 без остатка, а также выполнить само деление. Результаты приведены в таблице ниже.
| Число | Делится на 7 без остатка? | Результат деления |
|---|---|---|
| 7 | Да | 1 |
| 14 | Да | 2 |
| 21 | Да | 3 |
| 28 | Да | 4 |
| 35 | Да | 5 |
| 42 | Да | 6 |
| 49 | Да | 7 |
Используя правила, представленные в таблице, мы можем быстро определить, делится ли число на 7 без остатка, применить соответствующие действия и получить результат деления. Это очень полезно при выполнении математических операций, состоящих из большого количества делений на 7, так как упрощает и ускоряет процесс вычислений.
Вопрос-ответ

Как правильно расчитать делимое с делителем 7?
Чтобы расчитать делимое с делителем 7, нужно умножить делимое на 7 и затем разделить полученное число на 7. Например, если делимое равно 35, то результат будет 35*7/7 = 35.
Можно ли применять другие способы расчета делимого с делителем 7?
Да, кроме способа, описанного выше, можно использовать другой способ. Нужно умножить делимое на 1/7. Например, если делимое равно 49, то результат будет 49*1/7 = 49/7 = 7.
Как применять правило расчета делимого с делителем 7 на примере чисел с десятичной частью?
Если у числа с десятичной частью нужно применить правило расчета делимого с делителем 7, то десятичная часть числа нужно оставить без изменений, а целую часть умножить на 1/7. Например, если число равно 12.7, то результат будет 12 + 0.7*1/7 = 12 + 0.1 = 12.1.



