Наши глаза часто останавливаются на знакомых формах и образах, не задумываясь о глубине и сокровенных свойствах, которыми они обладают. Однако, за этими привычными очертаниями, в самой природе и в построении всех созданных нами предметов, скрываются удивительные законы искусства и гармонии.
Одним из таких законов является симметрия. Мы не всегда задумываемся о наличии или отсутствии осей симметрии вокруг нас, но они повсюду, как в живой природе, так и в искусстве.
Ось симметрии - это важное понятие, которое помогает нам воспринимать и классифицировать множество объектов и пространственных образов. Обладание осью симметрии придает рисунку или фигуре особую гармонию и баланс, а его отсутствие может создать ощущение динамизма и движения.
Основные свойства положения линии симметрии
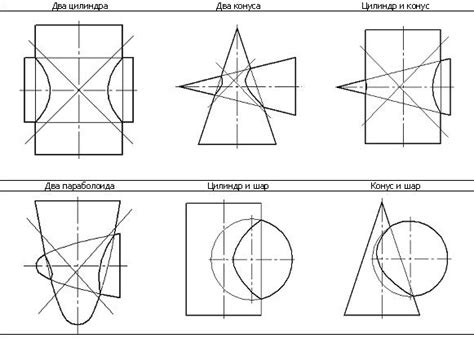
В данном разделе рассмотрены основные характеристики оси симметрии, о которых важно знать при изучении раскрашенных фигур. Эти свойства описывают положение и направление осей симметрии в различных фигурах, а также их роль в создании баланса и гармонии в изображении.
- Направление оси симметрии: В зависимости от направления, ось симметрии может быть вертикальной, горизонтальной или диагональной. Такое разнообразие позволяет достичь различных эффектов в расположении элементов фигуры и подчеркнуть их взаимосвязь.
- Положение оси симметрии: Ось симметрии может быть центральной, когда она проходит через центр фигуры, или неполной, проходящей через определенные точки или линии. Положение оси симметрии влияет на уровень симметрии и сбалансированности фигуры.
- Количество осей симметрии: Фигуры могут иметь одну или несколько осей симметрии, в зависимости от сложности и структуры изображения. Это важный аспект, определяющий степень симметрии и организации элементов фигуры.
- Роль оси симметрии: Оси симметрии являются основой для создания баланса и гармонии в раскрашенных фигурах. Они способствуют визуальному равновесию и созданию ощущения стабильности и совершенства в изображении.
Изучение основных характеристик оси симметрии позволяет понять важность этого элемента в создании эстетически привлекательных и сбалансированных фигур. Знание положения, направления и количества осей симметрии помогает находить гармоничные решения при создании и восприятии раскрашенных изображений.
Значение оси симметрии и ее роль в геометрии
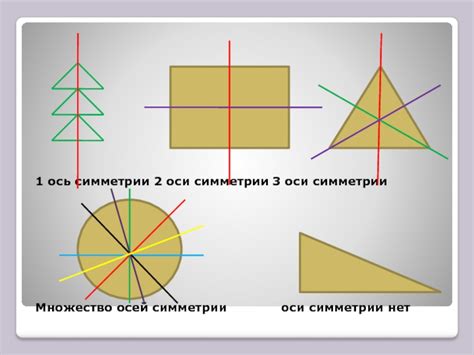
Ось симметрии представляет собой мнимую линию, которая разделяет фигуру на две симметричные половины. Это означает, что каждая половина фигуры является зеркальным отражением другой половины относительно оси симметрии. Благодаря оси симметрии мы можем увидеть и оценить равенство, баланс и гармонию в форме фигуры.
Ось симметрии не только придает фигуре эстетическую привлекательность, но также обладает практическим значением. Она помогает в расчетах и анализе формы. В многих областях науки и техники ось симметрии используется для создания симметричных и сбалансированных конструкций. Например, в архитектуре и дизайне ось симметрии часто используется для достижения гармонии и красоты в зданиях или предметах искусства.
| Важное | Существенное | Влиятельное |
|---|---|---|
| Значимое | Смысловое | Значительное |
| Заметное | Важное | Ощутимое |
| Значительное | Существенное | Весомое |
Математическое понятие осевой симметрии
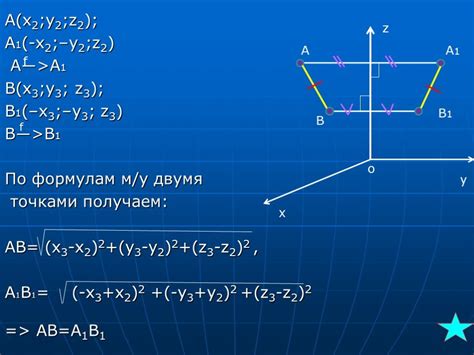
Ось симметрии проходит через центр симметрии фигуры и делит ее на две половины, которые являются точными копиями друг друга. Если взять одну из этих половин и отразить ее относительно оси симметрии, то получится исходная фигура.
Математически ось симметрии - это прямая линия, которая остается неподвижной при отражении фигуры по этой линии. Формально, для каждой точки P на фигуре существует такая точка P', симметричная ей относительно оси симметрии, что прямая, проходящая через эти две точки, перпендикулярна оси симметрии.
Осевая симметрия широко используется в геометрии и имеет множество приложений в различных областях. Понимание математического определения оси симметрии помогает анализировать и классифицировать фигуры, а также решать разнообразные геометрические задачи.
- Фигура с осью симметрии называется симметричной относительно этой оси.
- Фигура может иметь несколько осей симметрии или не иметь их вовсе.
- Линия, параллельная оси симметрии, также является осью симметрии для данной фигуры.
Фигуры, обладающие осевой однородностью
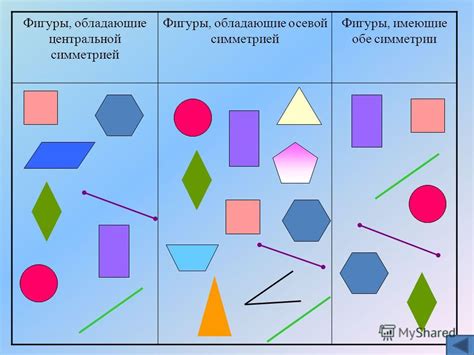
Осевая симметрия является фундаментальным понятием в геометрии и представляет собой свойство фигуры быть равной самой себе при отражении относительно некоторой прямой. Она делает такие фигуры яркими и эстетичными, добавляя им гармоничности и баланса.
В данном разделе мы рассмотрим несколько известных фигур, обладающих осевой симметрией, и исследуем их особенности. Например, вы узнаете о диагоналях, которые разделяют эти фигуры на две одинаковые части, и о способах определения оси симметрии при различной форме фигуры.
Мы также рассмотрим некоторые практические примеры применения фигур с осевой симметрией. Например, вы узнаете о симметричных крылах самолетов, о том как осевая симметрия используется в архитектуре, дизайне и в искусстве в целом.
Закончив чтение данного раздела, вы сможете лучше понять, как осевая симметрия определяет форму и внешний вид раскрашенных фигур, а также осознаете ее важность в различных областях человеческой деятельности.
Виды фигур с центральной осью равной формы
- Круглые фигуры: Круг - самая простая и понятная фигура с осью симметрии. Она обладает бесконечным количеством осей симметрии, так как любая линия, проведенная через ее центр, будет являться осью симметрии.
- Многоугольники: Некоторые многоугольники также могут обладать осью симметрии. Например, квадраты и прямоугольники имеют две параллельные оси симметрии - по диагонали и серединной линии.
- Специальные фигуры: Некоторые фигуры имеют особую симметрию. Например, сердце - символ любви и романтики - обладает осью симметрии, которая проходит по его вертикальной основе.
Ось симметрии играет важную роль во внешнем виде и структуре фигур. Наличие такой оси делает фигуры более гармоничными и сбалансированными. Даже несмотря на разнообразие форм и размеров, все эти фигуры имеют одну общую черту - наличие центральной оси симметрии, которая придает им особую красоту и гармонию.
Примеры симметрично раскрашенных фигур: гармония в отражениях
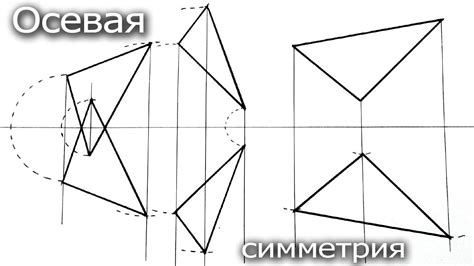
На примере этих фигур мы увидим, как ось симметрии влияет на внешний вид и ощущение асимметрии. Конечно, существуют и другие факторы, которые влияют на восприятие фигур, но ось симметрии является одним из ключевых аспектов, который мы хотим осветить в данном разделе.
- Прямоугольник: идеальное сочетание симметрии и практичности
- Круг: безупречная гармония в каждой точке
- Ромб: симметрия на стыке четырех углов
- Треугольник: обладает необычными осью симметрии
- Звезда: множество лучей с симметричным вращением
Эти фигуры подтверждают уникальное влияние оси симметрии на внешний вид и восприятие фигур. Примеры приведены с целью демонстрации, что красивые симметрично раскрашенные фигуры привлекают взгляд и создают впечатление особой гармонии. Каждая из этих фигур наглядно показывает, как ось симметрии подчеркивает ее красоту и элегантность, создавая визуальный баланс и привлекательность.
Фигуры с выразительными различиями в окраске

Некоторые фигуры, которые не обладают осью симметрии, могут повышать выразительность и оригинальность своего внешнего вида за счет необычных комбинаций цветов и расцветок.
Уникальные окраски обеспечивают фигуру богатством оттенков и тонов, создавая впечатление яркости или глубины. Обводка различных форм, покрытая сложными геометрическими узорами или бросающимися в глаза цветными пятнами, подчеркивает неповторимость изображения.
Раскрашенная поверхность без оси симметрии вызывает интерес и притягивает внимание к себе, создавая ощущение динамизма и движения. Сочетания ярких и насыщенных цветов в противоположность мягким и пастельным оттенкам эффектно подчеркивают контрасты и добавляют выразительности.
Уникальные комбинации цветов и рисунков на покраске фигуры без оси симметрии позволяют каждой фигуре выделиться из общего фона и стать ярким акцентом в пространстве. Возможности для экспериментов с цветовыми гаммами и текстурными решениями бесконечны, и каждая раскрашенная фигура может стать уникальным произведением искусства.
Особенности фигур, лишенных гармонии симметрии

От симметрии до несимметрии – это переход, по которому фигура обретает свою яркую индивидуальность и экспрессию. Фигуры без оси симметрии могут быть не только хаотичными и непредсказуемыми, но и порождать чувство динамики и движения. Именно в таких фигурах скрыта некая неизведанная гармония, которая может быть раскрыта в ходе наблюдения и анализа.
Фигуры без оси симметрии часто являются результатом творческого процесса, где автор сгущает краски и экспериментирует с формой. Они призваны вызывать эмоции и восприятие, а также способны притягивать взгляд своей оригинальностью. Нарушение симметрии может быть не только смелым решением, но и способом выделить фигуру среди других, придав ей индивидуальность и запоминающиеся черты.
Такие фигуры могут служить источником вдохновения для людей, стремящихся выразить свою индивидуальность и оригинальность через искусство или дизайн. Они вызывают мысли о том, что красота и гармония могут существовать и в несимметричном мире, что оставляет пространство для экспериментов и креативного подхода к созданию новых объектов и произведений искусства.
| Преимущества | Недостатки |
| Индивидуальность и оригинальность | Отсутствие гармонии и баланса |
| Привлекательность и внимание к деталям | Осложненное восприятие и ассимиляция |
| Возможность экспериментов и новаторства | Отличие от традиционных стандартов и норм |
Уникальные примеры фигур без способности отображать симметрию

Данный раздел посвящен удивительным и необычным фигурам, которые не обладают осью симметрии. Эти формы вызывают исключительный интерес и изучение, так как они представляют собой нестандартные и необычные образцы в мире геометрии.
1. Неправильный многоугольник Этот уникальный полигон имеет различные стороны и углы, что делает его неравномерным и лишает его способности отобразить ось симметрии. Этот класс фигур включает в себя треугольники, квадраты, пятиугольники и другие формы, в которых стороны и углы не равны друг другу. | 2. Кривая Коха Созданная математиком Хельгом Кохом, эта фрактальная кривая является одним из самых примеров форм без оси симметрии. Кривая Коха постоянно повторяет паттерн, добавляя все более маленькие и сложные детали. |
3. Эллипс Эллипс - это кривая, полученная при срезании конуса плоскостью, не проходящей через его вершину. У него есть две оси, но ни одна из них не является осью симметрии, так как наличие этих осей не означает, что форма будет симметричной относительно других линий. | 4. Фигуры случайной геометрии Некоторые фигуры могут быть созданы путем предоставления точек в случайном порядке без каких-либо определенных правил. В результате могут образовываться уникальные формы, которые не обладают никакой осью симметрии. Примером могут служить фрактальные формы или случайно созданные многоугольники. |
Вопрос-ответ

Может ли фигура иметь ось симметрии, если она раскрашена?
Да, фигура может иметь ось симметрии, несмотря на наличие раскраски. Ось симметрии является геометрической характеристикой фигуры и определяется ее формой и расположением элементов, независимо от их цвета.
Могут ли цвета, используемые для раскрашивания фигуры, влиять на наличие оси симметрии?
Цвета, используемые для раскрашивания фигуры, не влияют на наличие оси симметрии. Ось симметрии определяется исключительно геометрическими параметрами фигуры, такими как форма и расположение ее элементов.
Какие фигуры могут иметь ось симметрии, несмотря на наличие красок?
Фигуры, которые могут иметь ось симметрии, не зависимо от использования цветов, могут быть любой формы: круги, треугольники, прямоугольники, многоугольники или даже неправильные фигуры. Ось симметрии будет присутствовать, если форма фигуры может быть отражена относительно этой оси, вне зависимости от раскраски.
Могут ли две фигуры с одинаковой формой иметь разное количество осей симметрии из-за разных цветов?
Нет, две фигуры с одинаковой формой будут иметь одно и то же количество осей симметрии, даже если они раскрашены в разные цвета. Количество осей симметрии определяется формой фигуры, а не ее раскраской.
Что происходит с осью симметрии фигуры, когда ее раскрашивают?
Раскрашивание фигуры не влияет на ось симметрии. Ось симметрии остается на месте независимо от цветов, используемых для раскраски. Ось симметрии определяется геометрическими параметрами фигуры и остается неизменной при любой раскраске.



