Геометрия - это раздел математики, который изучает пространственные объекты и их свойства. Одним из основных понятий в геометрии является признак, который представляет собой характеристику или свойство геометрической фигуры.
Понимание значения признака в геометрии позволяет увидеть особенности фигур, определить их типы и классифицировать их по определенным критериям. Примерами таких признаков могут служить количество сторон, углов, радиус, диаметр и другие характеристики, которые могут быть использованы для описания и сравнения различных геометрических фигур.
Понимание и применение признаков в геометрии является важным элементом при решении задач на построение и анализ геометрических фигур, а также при изучении их свойств и взаимосвязей между ними.
Основное понятие признака

Так, например, одним из признаков треугольника является то, что он имеет три стороны и три угла. Этот признак помогает отличить треугольник от других геометрических фигур, таких как квадрат или круг.
Понимание и использование признаков является важным элементом в изучении геометрии, поскольку они позволяют систематизировать информацию о фигурах и объектах, делая возможным их классификацию и анализ.
Определение и роль
В геометрии признак могут называть любое свойство фигуры, с помощью которого можно идентифицировать данную фигуру или классифицировать его среди других. Понимание признаков играет ключевую роль в анализе геометрических объектов, поскольку они позволяют выявлять сходства и различия между фигурами, определять их свойства и решать задачи на основе этих данных. Важно уметь правильно определять и интерпретировать признаки, чтобы успешно работать с геометрическими объектами.
Примеры признаков в геометрии
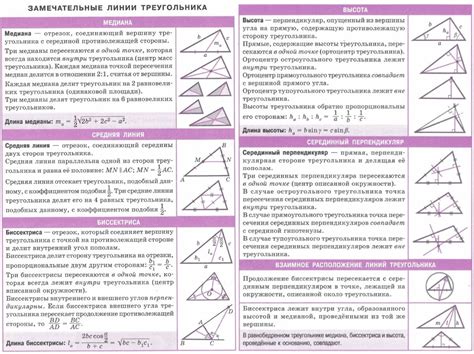
1. Признаки равенства треугольников:
а) Стороны равны, если соответствующие их стороны равны.
б) Углы равны, если соответствующие им углы равны.
2. Признак равенства прямоугольных треугольников:
Гипотенуза и катеты одного прямоугольного треугольника равны гипотенузе и катетам другого.
3. Признак равенства равнобедренных треугольников:
Две стороны равны, два угла при вершине равны.
Геометрические фигуры
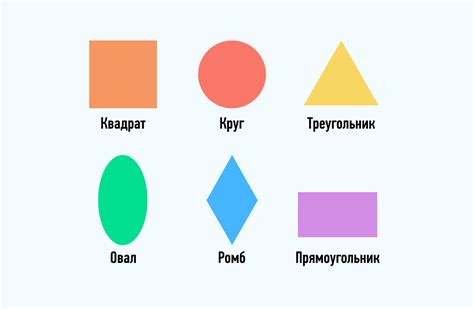
Геометрической фигурой называется область пространства, ограниченная кривой или поверхностью. К геометрическим фигурам относятся такие понятия, как окружность, треугольник, квадрат, прямоугольник и многоугольник.
Примеры геометрических фигур:
- Окружность: плоская фигура, состоящая из всех точек, равноудаленных от центра.
- Треугольник: фигура с тремя сторонами и тремя углами.
- Квадрат: четырехугольник, у которого все стороны равны и все углы прямые.
- Прямоугольник: четырехугольник, у которого противоположные стороны равны и все углы прямые.
- Многоугольник: фигура с произвольным числом сторон.
Свойства признаков
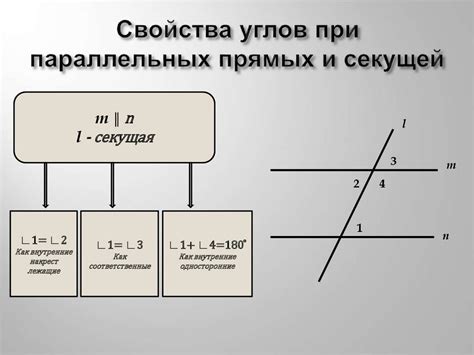
1. Существуют различные признаки в геометрии, которые играют важную роль при изучении форм и свойств геометрических фигур.
Например, признаки подобия треугольников позволяют устанавливать соответствие между сторонами и углами сходных фигур.
2. Признаки равенства геометрических фигур позволяют утверждать, что фигуры и их элементы совпадают по форме и размеру.
Также можно выделить признаки равенства треугольников, основанные на равенстве сторон и углов между ними.
3. Определение и использование признаков в геометрии помогает решать задачи на построение и анализ фигур, а также доказывать геометрические утверждения.
Понимание свойств признаков позволяет лучше понять геометрию, ее законы и особенности, и применять их на практике.
Влияние на решение задач

Понимание признака в геометрии играет важную роль в решении задач, связанных с построением фигур и определением их свойств. Знание конкретного признака позволяет определить, какие свойства обладают геометрические фигуры, и использовать их для решения задач по геометрии.
Например, если известно, что углы при основании равнобедренного треугольника равны, это позволяет нам определить другие углы в треугольнике и связанные с ним свойства, что упрощает задачу на определение геометрических параметров фигуры.
Практическое применение признаков

Еще одним практическим применением признаков является определение сходства или подобия фигур. По различным признакам, таким как соотношение сторон или углов, можно определить, являются ли две фигуры подобными.
| Пример | Признак | Применение |
|---|---|---|
| Стороны треугольника | Треугольник равносторонний, если все его стороны равны. | Помогает определить, является ли треугольник равносторонним. |
| Углы прямоугольника | Прямоугольник прямоугольный, если его диагонали перпендикулярны и равны. | Позволяет выяснить, является ли прямоугольник прямоугольным. |
Вопрос-ответ

Что такое признак в геометрии?
Признак в геометрии - это характеристика, свойство, или особенность, которая позволяет идентифицировать или описывать геометрические фигуры. Он может быть использован для определения определенного объекта или связей между объектами в геометрическом пространстве.
Какие примеры признаков существуют в геометрии?
Примерами признаков в геометрии могут служить: количество сторон и углов у фигуры, наличие определенных угловых или длинных соотношений, перпендикулярность сторон и т.д. Например, равенство всех углов треугольника или наличие двух пар равных сторон у четырехугольника - это также признаки, которые позволяют отличить одну фигуру от другой.
Как важно понимать значение признаков в геометрии?
Понимание значений признаков в геометрии существенно для корректного анализа и решения геометрических задач. Знание признаков позволяет уверенно определять и классифицировать различные фигуры, находить связи между ними, а также предсказывать их свойства и поведение в различных геометрических пространствах.



