Наклонная – одно из важных понятий в геометрии, которое играет ключевую роль при изучении треугольников и прямоугольных тел. Основание наклонной - это отрезок, соединяющий вершину угла с опущенной на него перпендикулярной точкой на противоположной стороне.
Интересно, что основание наклонной также определяет высоту треугольника, а именно расстояние от вершины угла до основания. Таким образом, основание наклонной имеет непосредственное влияние на свойства треугольника и позволяет легче решать задачи, связанные с геометрией.
Понимание основания наклонной является фундаментальным для успешного изучения геометрии и помогает углубить знания о треугольниках и их свойствах.
Что такое основание наклонной
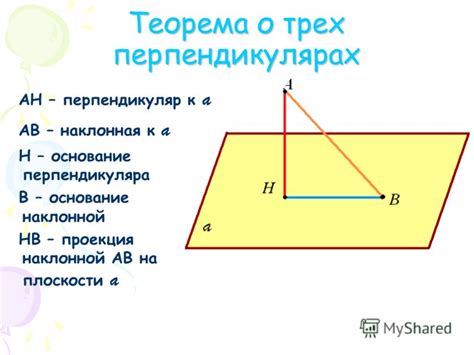
Иными словами, основание наклонной представляет собой сегмент прямой линии, на которой расположены начальная и конечная точки наклонной. Этот отрезок является базой для определения углов наклонной и ее направления.
Определение и объяснение в геометрии
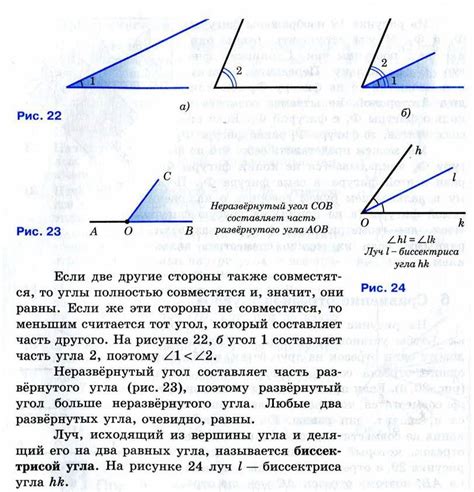
В геометрии основание наклонной играет важную роль при рассмотрении треугольников и задании их свойств. Оно определяет положение треугольника относительно горизонтали и позволяет выполнить различные геометрические операции.
Значение основания наклонной
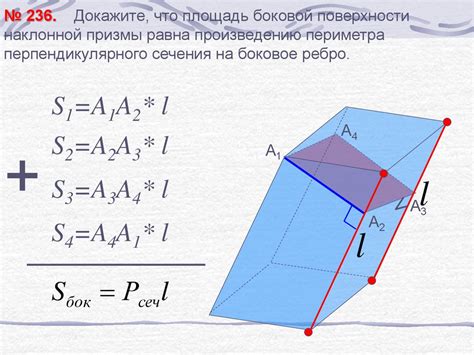
Важность в решении геометрических задач

Для правильного понимания геометрических задач необходимо уметь определять и использовать основание наклонной. С помощью этого элемента можно устанавливать отношения между различными частями фигур, находить длины сторон и углы, а также доказывать свойства различных геометрических фигур.
Таким образом, понимание и умение работать с основанием наклонной является необходимым навыком для успешного решения геометрических задач, а также для глубокого понимания принципов и свойств геометрии.
Как определить основание наклонной
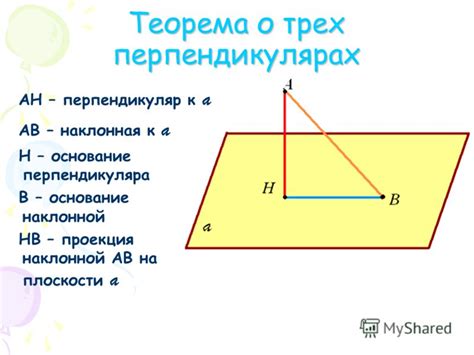
Чтобы определить основание наклонной, следует использовать знания о геометрических свойствах углов и отрезков на плоскости. Для этого можно:
- Построить наклонную и отметить ее вершину.
- На наклонной выбрать произвольную точку.
- Из вершины угла соединить данную точку с проведенной наклонной.
- Отрезок, полученный в результате соединения, будет служить основанием наклонной.
Таким образом, основание наклонной может быть определено как отрезок, соединяющий вершину угла с точкой на наклонной, через которую проведена линия.
Практические примеры и методы
В геометрии наклонная поверхность часто встречается в различных практических применениях. Например, знание основания наклонной позволяет строить крыши зданий, дорожные наклоны, а также использовать ее в рельефе местности.
Для определения угла наклона можно использовать различные методы, в том числе применение геодезических инструментов, измерение уклона с помощью уровня, а также математические расчеты с учетом геометрических основ.
| Пример | Метод |
|---|---|
| Строительство крыши | Измерение угла наклона с помощью специального уровня или планиметра |
| Дорожные наклоны | Использование геодезических инструментов для определения уклона дороги |
Таким образом, знание основания наклонной позволяет применять геометрические принципы в практических ситуациях, что является важным элементом при проектировании и строительстве различных объектов.
Свойства основания наклонной

- Основание наклонной равно основанию треугольника или многоугольника, к которому оно примыкает.
- Основание наклонной может быть как стороной треугольника, так и стороной многоугольника.
- При измерении основания наклонной нужно учитывать, что оно может быть как горизонтальным, так и наклонным относительно горизонтали.
- Основание наклонной влияет на высоту треугольника или многоугольника, именно поэтому определение основания наклонной критически важно для расчетов и конструкций в геометрии.
Какие характеристики важны для вычислений
Применение основания наклонной
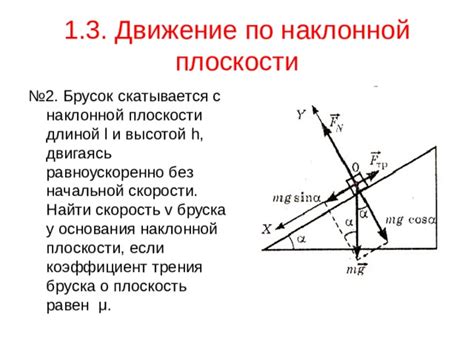
Основание наклонной играет ключевую роль в решении различных геометрических задач. Оно позволяет определить положение и направление наклонной относительно других элементов фигуры, а также вычислить различные углы и длины отрезков.
Одним из основных способов использования основания наклонной является определение высоты треугольника. Зная длину основания и угол наклона, можно рассчитать высоту треугольника с помощью тригонометрических функций.
Для нахождения площади треугольника также необходимо знать основание и высоту. Основание наклонной поможет определить высоту и, соответственно, рассчитать площадь фигуры.
Основание наклонной также используется при решении задач на построение многоугольников, где необходимо учитывать углы наклона сторон относительно основания.
Вопрос-ответ

Что такое основание наклонной?
Основание наклонной - это отрезок, который соединяет вершину наклонной с основанием. Он является частью треугольника и определяет его форму и положение.
Как определить основание наклонной в геометрии?
Для определения основания наклонной в геометрии нужно провести отрезок, соединяющий вершину наклонной с основанием, образуя тем самым боковую сторону треугольника. Основание наклонной определяется как одна из сторон этого треугольника.
Какое значение имеет основание наклонной в геометрии?
Основание наклонной в геометрии играет важную роль, поскольку оно определяет форму и положение треугольника. От его длины и расположения зависит величина углов и свойства треугольника в целом.
Можно ли построить наклонную без указания основания?
Нет, наклонную нельзя однозначно определить без указания основания. Основание наклонной является необходимым элементом для построения треугольника и определения его свойств.
Как выбрать правильное основание наклонной при построении треугольника?
При выборе основания наклонной при построении треугольника необходимо учитывать его длину, угол наклона, и положение относительно других сторон. Основание должно быть выбрано так, чтобы треугольник был правильным и его свойства были корректно определены.



