Интеграл – одно из важнейших понятий математического анализа. Он используется для нахождения площадей под кривыми, объемов тел и многих других задач. Возникает вопрос: можно ли разбить интеграл на два интеграла и как это повлияет на результат?
Интеграл – это предельное значение суммы, то есть величина, обладающая свойствами аддитивности. Таким образом, разбиение интеграла на два интеграла должно быть возможно. Однако, необходимо учитывать правила интегрирования и условия разбиения.
Существует несколько подходов к разбиению интеграла на два интеграла. Например, можно использовать метод замены переменных или разбить интеграл на сумму двух интегралов. Важно помнить, что изменение порядка интегрирования может привести к различным результатам, поэтому необходимо внимательно анализировать задачу.
Интегралы: важное понятие математики

Неопределенный интеграл – это обратная операция к дифференцированию, с помощью которой можно найти функцию, производная которой равна данной функции. Он представляет собой семейство функций, отличающихся на константу. Определенный интеграл, в свою очередь, позволяет находить площади под кривыми, объемы многогранников и другие величины.
Интегралы часто используются для решения задач, связанных с непрерывными величинами и функциями. Они являются мощным инструментом анализа и моделирования явлений в различных областях знаний.
Разбиение интеграла на части
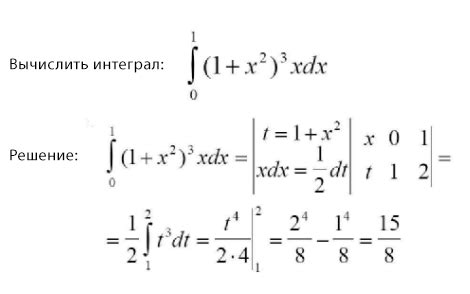
При определении интеграла функции одной переменной можно разбить интеграл на два интеграла, если функция имеет разрыв на конечном отрезке интегрирования. В таком случае необходимо выделять каждую часть интеграла, ограниченную разрывом, и вычислять их интегралы отдельно. Каждая из частей будет входить в общее значение интеграла на отрезке. Таким образом, разбиение интеграла на части позволяет учесть разрывы и получить правильное значение интеграла на отрезке интегрирования.
Метод разбиения интеграла

Метод разбиения интеграла представляет собой способ разделения области подынтегральной функции на две или более части для удобства вычисления интеграла. Этот метод особенно эффективен, когда область интегрирования имеет сложную форму или функция подынтегральная функция не может быть выражена аналитически. Путем разбиения области интегрирования можно упростить вычисление интеграла путем разбиения интеграла на несколько интегралов по подобластям или применения метода численного интегрирования.
Ограничения разбиения
При разбиении интеграла на два интеграла необходимо помнить о некоторых ограничениях:
- Разбиение должно быть правильным, то есть разбить отрезок на подотрезки равной длины.
- Интервалы разбиения должны быть обособлены от каких-либо особых точек и разрывов функции.
- Общее количество частей разбиения должно быть адекватно выбрано, чтобы обеспечить точность вычислений.
Возможность разбиения интеграла на два

Однако в некоторых случаях разбиение интеграла на два может быть невозможно из-за особенностей исходной функции или ее выражения. Поэтому необходимо внимательно анализировать функцию перед попыткой разбиения интеграла на два интеграла.
Примеры разбиения интеграла
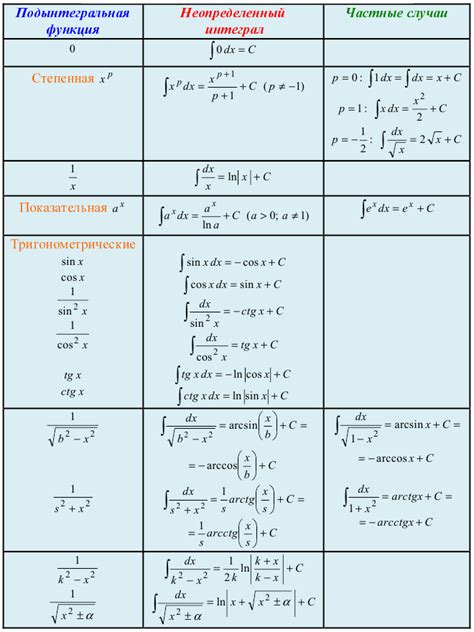
Предположим, что нужно вычислить определенный интеграл от функции f(x) на интервале [a, b]. Такой интеграл можно разбить на два интеграла, например, если функция f(x) имеет разный вид на двух подинтервалах [a, c] и [c, b].
Также интеграл можно разбить на два, чтобы удобнее было вычислять его значение, если функция f(x) имеет острые пики, точки разрыва или нетривиальные особенности на интервале интегрирования.
В некоторых случаях можно применить технику замены переменной, оставив в интеграле один или несколько слагаемых, а остальные вынести за пределы интеграла, что также приводит к разбиению исходного интеграла на более простые интегралы.
Плюсы и минусы разбиения интеграла
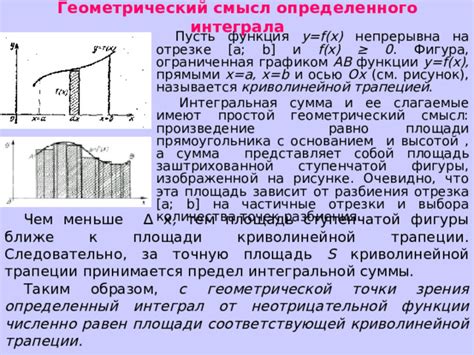
При разбиении интеграла на два интеграла есть как плюсы, так и минусы. Ниже приведены основные преимущества и недостатки данного подхода.
| Плюсы | Минусы |
|---|---|
| 1. Упрощение вычислений: разбиение интеграла на два интеграла иногда может упростить вычисления, особенно при наличии сложного подынтегрального выражения. | 1. Потеря точности: разбиение интеграла может привести к потере точности результата, особенно если переменная интегрирования находится на границе разбиения. |
| 2. "Распараллеливание" вычислений: возможность выполнять вычисления для каждого интеграла параллельно может ускорить процесс вычислений на многопроцессорных системах. | 2. Сложность анализа границ: не всегда легко определить границы для разбиения интеграла, что может усложнить анализ и вычисления. |
Вопрос-ответ

Как можно разбить интеграл на два интеграла?
Для разбиения интеграла на два интеграла необходимо применить метод интегрирования по частям, когда интегрируемая функция представляется как произведение двух функций.
Можно ли разбить определенный интеграл на два интеграла с разными пределами?
Да, определенный интеграл также можно разбить на два интеграла с разными пределами, применив соответствующие методы интегрирования.
Чем помогает разбиение интеграла на два интеграла?
Разбиение интеграла на два интеграла может упростить вычисление интеграла, помочь выделить отдельные части подынтегральной функции, что может ускорить процесс интегрирования и сделать решение более наглядным.



