Стационарные точки и точки экстремума являются ключевыми понятиями в математике и анализе. На первый взгляд они могут показаться схожими, но на самом деле имеют существенные различия.
Стационарная точка функции - это точка, в которой производная функции равна нулю или не существует. Она может быть как локальным минимумом, максимумом, так и точкой перегиба.
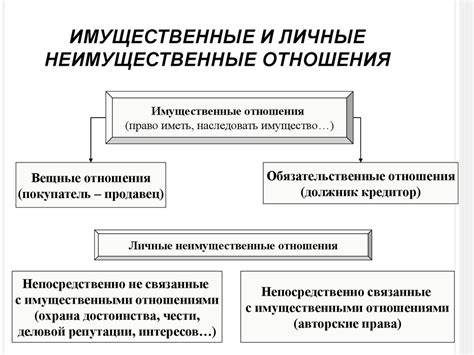
Точка экстремума функции - это точка, в которой функция принимает свое наибольшее (максимум) или наименьшее (минимум) значение. Это может быть как локальный, так и глобальный экстремум.
Что такое стационарные точки?

Существуют два типа стационарных точек: локальный минимум и максимум. Локальный минимум - это точка, в которой функция имеет наименьшее значение в некоторой окрестности данной точки. Локальный максимум - это точка, в которой функция имеет наибольшее значение в некоторой окрестности данной точки.
Определение и характеристики
Точки экстремума функции - это точки, в которых функция достигает локального минимума или максимума. При этом экстремумы могут быть как относительными (локальными), так и абсолютными (глобальными) - в зависимости от окрестности точки.
Важно отметить, что стационарные точки и точки экстремума функции могут пересекаться, но не всегда соответствуют друг другу. Например, точка перегиба не является точкой экстремума, но может быть стационарной.
Что такое точки экстремума?

Для того чтобы найти точки экстремума функции, необходимо произвести ее дифференцирование и найти корни уравнения производной функции. Точки, в которых производная равна нулю, могут быть точками экстремума. Происходит это потому, что в экстремальной точке функция может менять свое направление от убывания к возрастанию или наоборот.
Основные типы и свойства точек стационарности и точек экстремума

- Точка стационарности: это точка, в которой производная функции равна нулю. Точка стационарности может быть локальным минимумом, максимумом или седловой точкой.
- Точка экстремума: это точка, в которой функция достигает локального минимума или максимума. Точка экстремума характеризуется условиями первого и второго порядка.
Стационарные точки и точки экстремума играют важную роль при решении задач оптимизации и определении наилучшего значения функции.
Необходимо анализировать как первую, так и вторую производные функции, чтобы определить тип точки и ее свойства.
Как отличить стационарные точки и точки экстремума?

Стационарные точки - это точки, где производная функции равна нулю (f'(x) = 0) или не существует. Это могут быть минимумы, максимумы или точки перегиба кривой.
Точки экстремума - это точки, в которых функция достигает локального минимума или максимума. Экстремумы могут быть абсолютными (глобальными) или локальными.
Отличить стационарные точки от точек экстремума можно по значению второй производной функции. В точках экстремума вторая производная равна нулю или имеет определенный знак (положительный для локального минимума и отрицательный - для локального максимума).
Вопрос-ответ

Чем отличаются стационарные точки от точек экстремума?
Стационарные точки функции обладают нулевым значением первой производной функции, что говорит о том, что в этих точках функция не меняет свое значение. Точки экстремума - это точки, в которых функция принимает максимальное (локальное или глобальное) или минимальное значение. Точки экстремума являются частным случаем стационарных точек.
Как определить, что точка является стационарной?
Точка функции считается стационарной, если в этой точке производная функции равна нулю или если производная не существует. То есть, если изменение функции в этой точке не происходит или происходит в течение некоторого промежутка, то это стационарная точка.
Могут ли стационарные точки быть точками экстремума?
Да, стационарные точки могут быть как точками максимума, так и минимума функции. Если в стационарной точке значение функции достигает максимума или минимума, то эта точка является точкой экстремума.
Как связаны точки экстремума с выпуклостью функции?
Точки экстремума функции обычно связаны с кривизной функции в данной точке. В точке минимума функция обычно выпуклая, а в точке максимума - вогнутая. Таким образом, точки экстремума могут указывать на изменение выпуклости функции.



