Тангенс - это тригонометрическая функция, которая позволяет вычислить отношение противоположенного катета к прилежащему в прямоугольном треугольнике. Три корень из трех - это особенное число, которое можно представить в виде 3^(1/3) или ∛3. Рассмотрим, как можно вычислить тангенс этого числа с помощью математических формул.
Для вычисления тангенса 3 корня из 3 можно воспользоваться формулой: tg(x) = sin(x) / cos(x), где x - угол, sin(x) - синус угла, а cos(x) - косинус угла. Для тангенса 3 корня из 3 необходимо вычислить sin(∛3) и cos(∛3), а затем поделить sin(∛3) на cos(∛3).
Что такое тангенс трёх корней из трёх?

Таким образом, тангенс трёх корней из трёх - это значения тангенса угла, величина которого равна трем корням из трех. Оно может быть вычислено с помощью специальных таблиц или калькулятора.
Понятие тангенса и его значения

Тангенс угла 45 градусов равен 1 и также равен котангенсу угла 45 градусов. Тангенс острого угла в прямоугольном треугольнике всегда меньше 1, так как противолежащий катет меньше гипотенузы. Тангенс острого угла 30 градусов равен √3/3, а тангенс острого угла 60 градусов равен √3.
Как рассчитать тангенс 3 корня из 3?

Для вычисления тангенса 3 корня из 3 необходимо использовать математическую формулу:
tg(x) = sin(x) / cos(x)
Где x - угол, для которого нужно найти тангенс, в данном случае x = ∛3.
Вычислим:
- Сначала найдем синус и косинус угла ∛3.
- sin(∛3) ≈ 0.79
- cos(∛3) ≈ 0.61
- Подставляем значения sin(∛3) и cos(∛3) в формулу тангенса:
- tg(∛3) ≈ 0.79 / 0.61 ≈ 1.30
Таким образом, тангенс 3 корня из 3 примерно равен 1.30.
Формула для вычисления
Для расчета тангенса 3 корня из 3 можно воспользоваться следующей формулой:
tg(3√3) = sin(3√3) / cos(3√3)
Где sin(3√3) - значение синуса 3 корня из 3, а cos(3√3) - значение косинуса 3 корня из 3.
Примеры расчетов тангенса 3 корня из 3

Для того чтобы рассчитать тангенс 3 корня из 3, можно воспользоваться следующей формулой:
tan(3√3) = sin(3√3) / cos(3√3)
Для представления значения синуса и косинуса 3 корня из 3 необходимо использовать таблицы значений или специальные калькуляторы.
Например, если значение синуса 3√3 равно 0,866 и значение косинуса равно 0,5, то тангенс 3 корня из 3 будет:
tan(3√3) ≈ 0,866 / 0,5 ≈ 1,732
Практическое применение и примеры

Тангенс 3 корня из 3 может быть полезен при решении задач из различных областей, включая физику, инженерные науки и математику. Например, в задачах связанных с углами наклона, определением расстояний и длин отрезков, а также в построении графиков и моделировании.
Рассмотрим пример использования тангенса 3 корня из 3. Пусть дан треугольник с углом A, равным 3 корня из 3 градусов. Чтобы найти длину противолежащего катета к углу A, можно воспользоваться формулой тангенса: tg(A) = противолежащий катет / прилежащий катет. Таким образом, зная угол и значение тангенса, можно рассчитать неизвестную длину.
| Пример | Результат |
|---|---|
| Угол A = 3 корня из 3 градусов | tg(A) = tg(3√3) ≈ 0.577 |
| Значение тангенса | tg(3√3) = противолежащий катет / прилежащий катет |
| Пример расчета | Если прилежащий катет равен 1, то противолежащий катет будет примерно 0.577 |
Свойства тангенса 3 корня
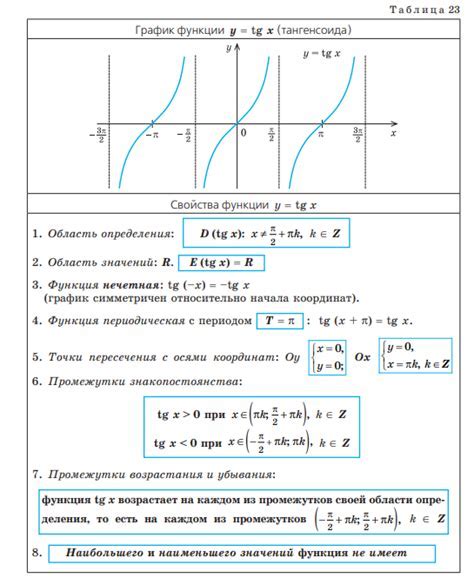
Свойства тангенса 3 корня из 3:
- Тангенс 3 корня из 3 – это отношение противоположной катеты к прилежащей стороне прямоугольного треугольника.
- Значение тангенса 3 корня из 3 может быть вычислено по формуле: tg(3√3) = sin(3√3) / cos(3√3).
- Тангенс 3 корня из 3 зависит от значений синуса и косинуса 3 корня из 3.
Вопрос-ответ

Каковы основные формулы для вычисления тангенса 3 корня из 3?
Основная формула для вычисления тангенса угла α звучит так: tg(α) = sin(α) / cos(α). Для нахождения тангенса 3 корня из 3 можно воспользоваться формулой тангенса суммы углов: tg(3√3) = tg(π/6) = sin(π/6) / cos(π/6) = (√3) / 2 / (1 / 2) = √3.
Как выглядят расчеты для нахождения тангенса 3√3?
Для нахождения тангенса 3√3 нужно использовать значение синуса и косинуса угла 30 градусов (или π/6 радиан), так как 3√3 является косинусом угла 30 градусов. Подставив значения синуса и косинуса в формулу тангенса, получим tg(3√3) = tg(π/6) = sin(π/6) / cos(π/6) = (√3) / 2 / (1 / 2) = √3.
Какие свойства обладает тангенс 3 корня из 3?
Тангенс 3 корня из 3, равный √3, обладает следующими свойствами: он положителен в первом и третьем квадрантах, а также является периодической функцией с периодом π. Тангенс является отношением синуса косинуса, поэтому его значения ограничены определенным диапазоном.
Какую роль играет тангенс 3 корня из 3 в математике?
Тангенс 3 корня из 3 является одним из значений трехгранной функции тангенса, которая широко используется в математике и физике для решения различных задач, например, при вычислении углов, определении расстояний и траекторий движения. Тангенс играет важную роль в тригонометрии и математическом анализе.



