Отрицательные числа - это понятие, которое может вызывать множество эмоций и ассоциаций: от тоски и грусти до беспокойства и неопределенности. Но что происходит, когда мы пытаемся сложить два отрицательных числа? Что проявляется в этой математической операции, и может ли она иметь осмысленный результат?
Каждый из нас знаком с понятием сложения в математике - два числа сходятся вместе, создавая новое значение. В то же время отвергая традиционные представления о сложении, отрицательные числа открывают перед нами совершенно иной мир, где правила и ожидания требуют переосмысления.
Но какие результаты может показать сложение двух отрицательных чисел? Этот вопрос заслуживает нашего внимания, поскольку он вызывает не только математическую, но и философскую бурю в наших умах. Возможно, в этой операции мы найдем гармонию в противоположности и расширим наше понимание числовых отношений. Давайте попробуем разобраться вместе!
Комплексное сложение двух отрицательных чисел

В данном разделе мы рассмотрим процесс комплексного сложения, осуществляемого с помощью математических операций над двумя числами, которые относятся к отрицательному диапазону.
Когда мы говорим о "отрицательных числах", мы имеем в виду числа, которые находятся ниже нулевой отметки на числовой оси. Вместе с тем, комплексное сложение предполагает работу с числами, которые имеют вещественную и мнимую составляющие.
Такое сложение выполняется путем суммирования соответствующих вещественных и мнимых частей отрицательных чисел. Обычно вещественная часть отрицательного числа записывается с отрицательным знаком, а мнимая часть представляется в виде выражения с обычным положительным знаком.
| Пример | Результат |
|---|---|
| (-2 - 3i) + (-5 + 4i) | -7 + i |
| (-1 + 2i) + (-4 - 3i) | -5 - i |
| (-3 - 5i) + (-2 + 7i) | -5 + 2i |
Итак, комплексное сложение двух отрицательных чисел заключается в суммировании их вещественной и мнимой частей для получения комплексного числа с отрицательной вещественной и положительной мнимой частями.
Отрицательные числа в математике: основные понятия и характеристики

Рассмотрим важное понятие отрицательных чисел в области математики. Они представляют собой числа, отражающие отрицательные значения или убывающие значения всего, что можно измерить, подсчитать или выразить с помощью чисел. В отличие от положительных чисел, которые обозначают количества или значения, отрицательные числа указывают на отсутствие или уменьшение количества или значения.
В подавляющем большинстве случаев отрицательные числа представляются с помощью отрицательного знака "минус", который указывает на отрицательное значение. Например, -5. Однако, также возможно использование других способов обозначения отрицательных чисел, например, в виде круглых скобок с отрицательным знаком перед числом, таким образом: (-5).
Отрицательные числа позволяют нам работать с отрицательными значениями, долгами, убывающими темпами и другими ситуациями, в которых отсчет идет в обратном направлении. Например, если мы имеем температуру -10°С, это означает, что температура ниже нуля (т.е., ниже обычного уровня). Также, отрицательные числа могут использоваться для обозначения убывания количественных значений, например, при уменьшении скорости движения.
- Отрицательные числа имеют свои особенности и свойства, которые позволяют нам выполнять арифметические операции с этими числами.
- Сложение двух отрицательных чисел приводит к получению отрицательного результата, более малого по модулю значения. Например, (-4) + (-3) = (-7), где результат -7 является отрицательным числом, так как значение меньше нуля и меньше по модулю, чем -4 и -3.
- Учитывая особенности отрицательных чисел, можно сказать, что их сложение влечет за собой "уменьшение" или "сокращение" количества или значения.
- Отрицательные числа обладают своими правилами для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Знание и понимание этих правил и особенностей позволяет нам корректно выполнять математические операции с отрицательными числами.
Итак, отрицательные числа являются важным понятием в математике, позволяющим нам работать с отрицательными значениями и убывающими темпами. Понимание основных понятий и свойств отрицательных чисел позволяет нам выполнять арифметические операции с этими числами и применять их в различных практических ситуациях.
Правила сложения чисел с разными знаками

В математике существуют определенные правила для сложения чисел с положительными и отрицательными знаками. При сложении положительного и отрицательного чисел необходимо учитывать их знаки и выполнять соответствующие операции. Давайте рассмотрим эти правила более подробно.
Когда мы складываем числа с одинаковыми знаками, получаем новое число со знаком, который совпадает с знаком слагаемых. Например, если мы складываем положительное число с другим положительным числом, результат также будет положительным. Аналогично, если мы складываем отрицательное число с другим отрицательным числом, результат будет отрицательным.
Однако, когда мы складываем числа с разными знаками, происходит некоторая особенность. Если положительное число больше отрицательного, то результат будет положительным числом и его величина будет равна разнице между этими числами. Например, если мы складываем число 5 и -3, результат будет положительным числом 2.
Если же отрицательное число больше по модулю, то результат будет отрицательным числом и его величина будет равна разнице между модулем отрицательного числа и положительным числом. Например, если мы складываем число -7 и 4, результат будет отрицательным числом -3.
| Знак первого числа | Знак второго числа | Результат |
|---|---|---|
| Положительное | Положительное | Положительное |
| Отрицательное | Отрицательное | Отрицательное |
| Положительное | Отрицательное (по модулю) | Положительное |
| Отрицательное (по модулю) | Положительное | Отрицательное |
Таким образом, правила сложения положительных и отрицательных чисел помогают определить знак и величину результирующего числа. Важно помнить и применять эти правила при выполнении операций с числами разных знаков.
Что происходит при суммировании двух чисел со знаком "+"?

При сложении двух положительных чисел мы выполняем операцию, которая приводит к объединению двух положительных величин. Данное действие проводится с целью определения общей суммы двух положительных чисел. При сложении положительных чисел результатом будет положительное число. Это означает, что общая сумма двух положительных величин будет также положительной.
- Проводим операцию сложения
- Объединяем два положительных числа
- Получаем положительное число в качестве результата
Например, если мы сложим числа 3 и 4, результатом будет число 7. Таким образом, сумма двух положительных чисел равна положительному числу, которое является суммой исходных положительных величин.
Примечательности сложения отрицательных чисел

При проведении сложения двух отрицательных чисел в математике существуют определенные особенности и принципы, которые важно учитывать. Это важный аспект исследования международных математических стандартов и концепций, помогающих понять и объяснить, как два отрицательных числа взаимодействуют друг с другом.
При сложении отрицательных чисел возникает явление, которое называется "отрицательная сумма". Оно характеризуется тем, что в результате сложения двух отрицательных чисел получается число, которое также является отрицательным. Это связано с особенностями числовой оси и представлением чисел в отрицательной форме.
Примечательно, что сложение отрицательных чисел можно представить с помощью понятия долга и должника. Представим, что у нас есть должник, сумма его долга отрицательна, и к нему прибавляем сумму еще одного должника, также имеющего отрицательный долг. В результате сложения долгов, общая сумма будет еще более отрицательной, то есть должник будет иметь еще больший долг.
Также важно учитывать, что результат сложения двух отрицательных чисел можно интерпретировать как удаление определенной суммы из общего количества. Например, если у нас имеется отрицательное число, представляющее задолженность, и к нему прибавляется отрицательное число, представляющее часть этой задолженности, то результатом сложения будет сокращение общей задолженности.
Таким образом, понимание особенностей сложения отрицательных чисел является важной составляющей в изучении математики и помогает детальнее разобраться в процессе арифметических операций и их результатами.
Понятие абсолютной величины отрицательного числа
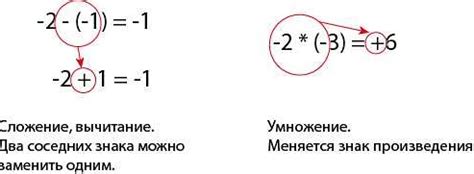
В математике существует понятие абсолютной величины, которое применяется к числам независимо от их знака. В данном разделе мы рассмотрим абсолютную величину отрицательных чисел и разъясним ее значение и свойства.
Когда мы говорим об абсолютной величине отрицательного числа, мы учитываем только его числовую величину, независимо от того, является оно отрицательным или положительным. В отличие от понятия знака числа, которое указывает на его направление (вправо или влево на числовой оси), абсолютная величина фокусируется именно на его числовом значении.
Обычно абсолютную величину отрицательного числа обозначают двойными вертикальными чертами, например, |-5|. Это означает, что абсолютная величина отрицательного числа 5 равна положительному числу 5.
Абсолютная величина отрицательных чисел полезна при сравнении и упорядочивании числовых значений. Она помогает определить, какое из двух отрицательных чисел больше или меньше по модулю. Например, |-2| будет меньше, чем |-1|, поскольку абсолютная величина отрицательного числа 2 меньше, чем абсолютная величина отрицательного числа 1.
Таким образом, понятие абсолютной величины отрицательного числа позволяет нам учитывать только числовое значение и игнорировать его знак, что является полезным инструментом в решении различных математических задач и проблем.
Примеры суммирования отрицательных чисел

В данном разделе приведены примеры сложения чисел, которые имеют отрицательное значение. Будут рассмотрены ситуации, когда отрицательные числа складываются как сами по себе, так и с положительными числами, с целью понять, как происходит операция сложения в таких случаях.
| Отрицательное число 1 | Отрицательное число 2 | Сумма |
|---|---|---|
| -5 | -3 | -8 |
| -10 | -7 | -17 |
| -2 | -9 | -11 |
Из представленных примеров видно, что когда два отрицательных числа складываются, получаемое число также имеет отрицательное значение и его величина равна сумме модулей этих чисел. Это означает, что при сложении двух отрицательных чисел их абсолютные величины складываются, а знак результата сохраняется отрицательным.
Возможные особенности при сложении отрицательных чисел в системе счисления

При выполнении операции сложения отрицательных чисел в системе счисления возникают некоторые особенности, которые отличаются от обычного сложения положительных чисел.
Во-первых, при сложении двух отрицательных чисел с одинаковым знаком, получается число с тем же знаком. Например, -5 + (-3) = -8. Это связано с правилами сложения чисел с отрицательным знаком.
Во-вторых, при сложении отрицательного числа соответствующего положительного числа, возникает разница в итоговом знаке результата. Например, -5 + 3 = -2. В данном случае, отрицательное число -5 сокращается на положительное число 3, что приводит к уменьшению величины числа со знаком минус.
Также следует обратить внимание на переход через ноль при сложении двух отрицательных чисел. Если сумма отрицательных чисел превышает модуль числа, полученного при сложении, то происходит переход через ноль и получается положительное число. Например, -3 + (-5) = 2.
Важно помнить, что при сложении отрицательных чисел в системе счисления учитывается величина чисел и их соотношение, что приводит к особым свойствам результатов.
Роль скобок при сложении отрицательных чисел

Скобки, в данном контексте, выполняют не только функцию обозначения математической операции, но и позволяют уточнить порядок выполнения действий. Они помогают явно определить, какие числа должны быть сложены друг с другом, а какие нет, чтобы избежать ошибок в вычислениях и получить правильный ответ.
Использование скобок при сложении отрицательных чисел также позволяет улучшить понимание промежуточных шагов вычислений. Они помогают наглядно представить, как происходит сложение чисел, особенно в случаях, когда присутствуют разные знаки чисел и множество скобок.
Без использования скобок при сложении отрицательных чисел мы можем неправильно определить порядок выполнения операций, что приведет к неверному результату. Это связано со спецификой правил математических операций, где сложение имеет приоритет над вычитанием. Правильное расстановка скобок помогает избежать путаницы и сделать вычисления более понятными.
Практическое применение сложения отрицательных чисел в реальной жизни

Когда в реальном мире возникают ситуации, требующие сложения отрицательных чисел, это может быть связано с финансами, температурой или расстояниями. В таких случаях правильное выполнение сложения отрицательных чисел может помочь нам осуществить корректные вычисления и принимать информированные решения.
Применение сложения отрицательных чисел можно найти в финансовом планировании, например, при рассчете бюджета с отрицательными значениями расходов или долгов. Сложение отрицательных чисел позволяет нам корректно учесть требуемые платежи или расходы и правильно спланировать свои финансы.
Другим примером практического применения сложения отрицательных чисел является измерение низких температур. Когда мы имеем дело с отрицательными значениями температуры, сложение отрицательных чисел позволяет нам точно определить температурное изменение или разницу между двумя отрицательными значениями. Это очень полезно для метеорологов, а также для тех, кто работает в области холодильного оборудования или климатической техники.
Еще одним примером применения сложения отрицательных чисел является определение расстояния. В навигации и геодезии нередко возникает необходимость учитывать отрицательные значения расстояний. Сложение отрицательных чисел позволяет нам правильно определить расстояние, учитывая его направление и ориентацию.
Вопрос-ответ

Какой результат сложения двух отрицательных чисел?
Результат сложения двух отрицательных чисел всегда будет отрицательным числом. Например, если сложить -5 и -3, получится -8.
Если сложить два отрицательных числа, получится положительное число?
Нет, результат сложения двух отрицательных чисел всегда будет отрицательным числом. Неважно, сколько чисел вы суммируете, знак минус сохраняется. Например, -7 + (-4) = -11.
Что будет, если сложить два отрицательных числа с разными значениями?
Если сложить два отрицательных числа с разными значениями, результат будет отрицательным числом, которое зависит от значений чисел и порядка сложения. Если первое число по модулю больше, то результат будет ближе к нему. Например, -9 + (-2) = -11.
Можно ли получить положительный результат от сложения двух отрицательных чисел?
Нет, сложение двух отрицательных чисел всегда дает отрицательный результат. Математически это объясняется тем, что отрицательные числа на числовой прямой находятся левее нуля, а результат сложения всегда будет в этой области.



