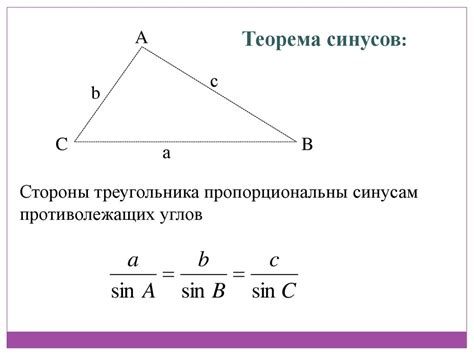
Тригонометрия – раздел математики, изучающий связь между углами и сторонами треугольников. Синус, косинус и тангенс – основные тригонометрические функции, играющие важную роль не только в математике, но и в различных областях науки и техники.
Синус учит нас определять отношение противоположной стороны к гипотенузе в прямоугольном треугольнике. Косинус позволяет находить отношение прилежащей стороны к гипотенузе. Тангенс же показывает отношение противоположной стороны к прилежащей. Эти функции необходимы для решения задач с углами, расстояниями, скоростями и других параметров.
Практическое применение синусов
Синусы широко применяются в различных областях науки и техники. Например, в физике они используются для расчета колебаний, напряжений и деформаций в различных системах. В астрономии синусы помогают определять положение небесных тел. В инженерии они применяются при проектировании строительных конструкций, машин и механизмов.
Пример: При анализе колебаний маятника с помощью синусов можно определить период колебаний и амплитуду движения, что важно при проектировании маятниковых часов или других механических устройств.
Синусы в геодезии и астрономии

В геодезии синусы используются для решения задач связанных с измерением углов и расстояний на поверхности Земли. Например, с помощью тригонометрических функций, включая синусы, определяются высоты гор и расстояния между ними.
В астрономии синусы также играют важную роль. Например, для вычисления положения небесных тел используется сферическая тригонометрия, где синусы помогают определить углы между звездами и планетами.
| Использование синусов в геодезии | Использование синусов в астрономии |
|---|---|
| Расчет высот гор и глубин водоемов | Определение положения небесных тел |
| Измерение расстояний на поверхности Земли | Вычисление долготы и широты |
Использование косинусов в технике
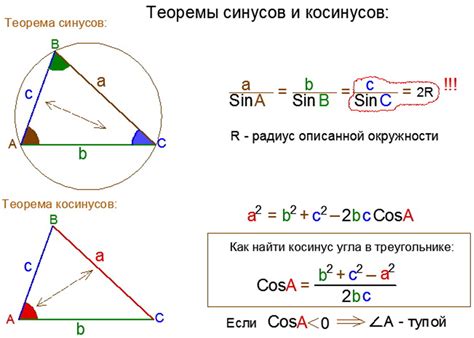
Например, при проектировании строительных конструкций, инженеры используют косинусы для определения углов наклона кровли, стен или опор.
Также косинусы находят применение в радиотехнике и электронике при расчете фазовых сдвигов, например, при настройке антенн или при синхронизации сигналов.
Кроме того, в авиации косинусы используются для решения навигационных задач, таких как расчет курса или определение угла наклона самолета.
Таким образом, знание и применение косинусов в технике позволяет профессионалам эффективно решать сложные инженерные задачи и обеспечивать надежную работу различных технических устройств.
Косинусы при расчете угловой скорости
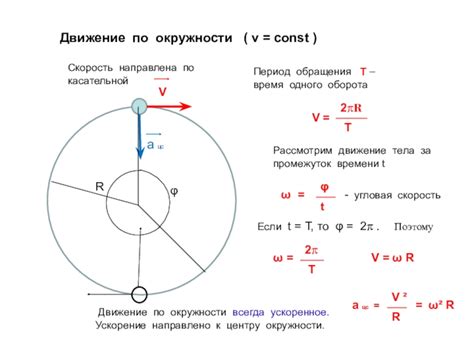
При решении задач, связанных с движением вращающегося тела, косинусы играют важную роль при расчете угловой скорости. Угловая скорость определяется как изменение угла поворота тела за единицу времени.
Для расчета угловой скорости можем использовать следующую формулу:
| Угловая скорость (ω) | = | Скорость точки вращения (Vт) | × | Радиус вращения (R) | / | Косинус угла между линией радиуса и направлением скорости точки (cosθ) |
|---|
Здесь косинус угла между линией радиуса и направлением скорости точки помогает учесть угол наклона точки к линии радиуса, что существенно для корректного определения угловой скорости вращающегося объекта.
Тангенсы в инженерии и архитектуре
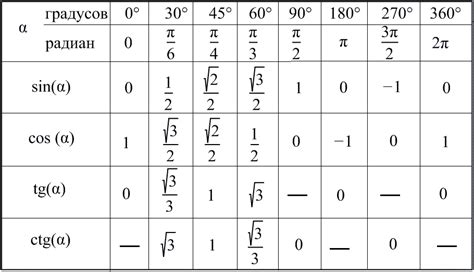
Тангенс как тригонометрическая функция широко используется в инженерии и архитектуре для решения различных задач. Например, при проектировании строений инженеры часто применяют тангенс для расчета угла наклона кровли, чтобы обеспечить оптимальное стекание дождевой воды. Также тангенс используется при проектировании дорог, мостов и других инженерных сооружений для определения уклона и высоты.
В архитектуре тангенс помогает определить нужный угол наклона крыши, чтобы дом или здание выглядело гармонично и соответствовало архитектурному стилю. Также тангенс используется при создании интерьеров, чтобы правильно расположить мебель или подобрать уклон стен для оптимального освещения.
Вопрос-ответ

Зачем нужны синусы, косинусы и тангенсы в математике?
Синусы, косинусы и тангенсы являются тригонометрическими функциями, которые широко используются в математике для расчетов в различных областях. Они помогают решать задачи связанные с углами, трактовать геометрические задачи, а также применяются в физике, инженерии, статистике и других науках.
Какие конкретные практические применения у синусов и косинусов?
Синусы и косинусы используются в навигации, геодезии, строительстве, механике, физике и других областях. Например, они помогают определять высоту объектов, расстояния между точками, силы векторов, колебания и многое другое.
Какие примеры применения тангенсов в повседневной жизни?
Тангенсы тоже находят свое применение в различных задачах. Например, они могут использоваться при расчетах наклона поверхности, угла наклона склона, в технике безопасности при подъеме на высоту и в других ситуациях, где важно знать углы наклона.
Какие практические плюсы дает знание тригонометрии для обычного человека?
Знание тригонометрии, включая синусы, косинусы и тангенсы, помогает в повседневных ситуациях, например, при ориентации на местности, при выполнении строительных работ, при изучении физических процессов или применении алгоритмов обработки сигналов.



