В физике существуют различные подходы к определению объема вещества. Один из них предполагает рассмотрение вещества вне зависимости от его массы. Такой подход имеет свои особенности и позволяет углубить наше понимание свойств вещества и его структуры.
Определение объема без учета массы открывает перед нами необычные возможности. На первый взгляд может показаться, что объем и масса тесно связаны и нельзя рассматривать их отдельно. Однако, исследования показывают, что объем вещества может иметь свои свойства и изменяться независимо от массы.
Уникальные методы определения объема в физике без учета массы позволяют сохранить полное понимание свойств и характеристик вещества. Мы можем изучать объемность вещества, испытывать его влияние на окружающую среду и исследовать его взаимодействие с другими материалами.
Часто примеры из реальной жизни используются для наглядного представления такого подхода. Например, растения растут и расширяются в объеме несмотря на изменение своей массы. Или воздух, окружающий нас, может изменять свой объем при изменении условий, но его масса остается неизменной.
Метод архимедова принципа: определение объема плавающих тел

Принцип Архимеда можно объяснить следующим образом: когда тело погружается в жидкость, оно вытесняет определенный объем этой жидкости. Этот объем можно рассматривать как объем плавающего тела. Поэтому, если мы знаем плотность жидкости и массу тела, мы можем определить его объем.
Для определения объема плавающих тел по методу архимедова принципа, мы можем использовать следующие шаги:
- Измерить массу плавающего тела с помощью весов.
- Погрузить тело в жидкость и измерить силу, с которой оно всплывает. Эту силу можно измерить, используя плотнометр или другие специальные инструменты.
- Используя плотность жидкости, рассчитать объем вытесненной телом жидкости с помощью формулы, основанной на принципе Архимеда.
Таким образом, метод архимедова принципа позволяет оценить объем плавающих тел без необходимости учитывать их массу. Это полезный метод, который может быть применен в различных областях физики, таких как гидростатика, гидродинамика и аэродинамика.
Метод гидростатического давления: измерение объема жидкостей и газов
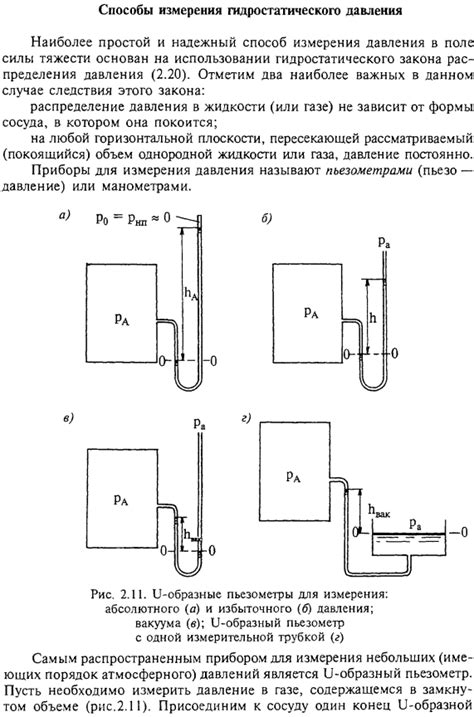
Для точного измерения объема жидкостей с использованием гидростатического давления необходимо знать плотность среды и глубину погружения измерительного инструмента в жидкость. Путем измерения давления на разных глубинах можно определить объем источника жидкости.
При измерении объема газов с использованием гидростатического давления используется закон Паскаля, согласно которому давление на любой глубине одинаково во всех направлениях. Для определения объема газа необходимо использовать герметичный сосуд с известным объемом и измерить изменение давления при введении газа.
- Преимущества этого метода: точность измерений, независимость от массы вещества, применимость как для жидкостей, так и для газов.
- Ограничения метода: необходимость знания плотности среды, требование герметичности измерительного сосуда.
- Пример применения: определение объема неизвестной жидкости в лаборатории или измерение объема газа в контролируемых условиях.
Метод геометрических расчетов: определение объема регулярных тел

В данном разделе мы рассмотрим метод геометрических расчетов, который позволяет определить объем регулярных тел без учета их массы. Узнаем, каким образом можно использовать геометрические свойства этих тел для расчетов и приведем несколько примеров применения данного метода.
Геометрические расчеты позволяют определить объем регулярных тел на основе их формы и размеров. Регулярные тела характеризуются определенными геометрическими свойствами, такими как количество граней, ребер и вершин, а также одинаковые размеры граней и углы между ними. Используя эти свойства, можно применить соответствующие формулы и выразить объем тела в зависимости от его характеристик.
Один из примеров регулярного тела - куб. Куб имеет шесть равных граней, каждая из которых является квадратом. Углы между гранями куба также равны между собой. С помощью геометрических расчетов мы можем определить объем куба, основываясь на длине его стороны.
Еще одним примером регулярного тела является сфера. Сфера имеет форму, близкую к идеальной округлости, и все ее точки равноудалены от ее центра. Для расчета объема сферы используются формулы, основанные на радиусе сферы.
Метод геометрических расчетов позволяет определить объем регулярных тел без учета их массы. Используя геометрические свойства тел, мы можем применить соответствующие формулы и выразить объем в зависимости от их характеристик. Понимание данного метода и его применение в решении задач позволяют более точно оценивать объем регулярных тел в физике.
Метод дифференциальной популярности: определение пространственных размеров сложных форм

Для анализа и измерения сложных форм, таких как фигуры живых организмов, естественных образований или архитектурных сооружений, в физике используется метод дифференциальной популярности. Этот метод позволяет определить пространственные размеры объектов, не привлекая при этом к учету их массы.
Одной из основных идей метода дифференциальной популярности является выделение значимых особенностей формы объекта и их сравнительный анализ. Путем измерения различных характеристик, таких как длина, ширина, высота, радиусы, углы и кривизны, можно получить информацию о пространственных размерах сложных форм. Такой подход позволяет описать и классифицировать объекты с высокой точностью, даже не задавая конкретных определений их объема.
Для реализации метода дифференциальной популярности необходимо использовать современные инструменты и приборы, такие как лазерные сканеры, компьютерное зрение, 3D-моделирование и анализ данных. Эти технологии позволяют получить точные измерения и визуализацию сложных форм, что способствует более глубокому пониманию их геометрических характеристик.
Применение метода дифференциальной популярности находит широкое применение в различных областях, таких как биология, геология, архитектура и инженерия. Например, в биологии данный метод может быть использован для определения размеров органов и тканей в организмах, исследования пространственной структуры молекул ДНК и РНК. Архитектурные и инженерные применения метода дифференциальной популярности включают измерение сложных геометрических форм зданий, мостов и технических конструкций.
Таким образом, метод дифференциальной популярности является эффективным инструментом для определения и измерения пространственных размеров сложных форм. Он основывается на анализе значимых характеристик объектов и позволяет классифицировать их с высокой точностью. Применение данного метода в различных областях знаний демонстрирует его широкий потенциал и перспективы для дальнейших исследований и разработок.
Пример использования метода дисплейсмента: определение объема корабля

| Характеристика каркаса | Значение |
|---|---|
| Длина киля | 25 м |
| Ширина корабля | 10 м |
| Высота борта | 5 м |
Для определения объема корабля по методу дисплейсмента необходимо измерить геометрические характеристики его каркаса, такие как длина, ширина и высота. В данном примере длина киля составляет 25 метров, ширина корабля - 10 метров, высота борта - 5 метров. Далее, используя эти значения, можно применить формулу для расчета объема дисплея и получить точное значение объема данного корабля.
Роль океанографии в измерении содержания воды в океане

Океанография использует разнообразные инструменты и методы для сбора данных о физических, химических и биологических свойствах океанов. Одной из ключевых областей ее исследования является гидрография - наука о измерении и описании физических свойств воды в океане.
Одним из методов, используемых океанографами для определения объема воды в океане, является гидрографическое исследование. В ходе этого исследования производится наблюдение за свойствами водной среды, проводятся измерения температуры, солености и плотности воды. Эти данные затем используются для расчета объема и общего количества воды в океане.
Другим методом, применяемым для определения объема воды, является зондирование океана с помощью зондов. Зонды, спускаемые в океан, позволяют измерить различные физические параметры воды на разных глубинах. После сбора данных специалисты океанографии проводят анализ полученной информации, что позволяет им определить объем воды и поверхностных водных масс в океане.
Таким образом, океанография играет важную роль в измерении объема воды в океане, помогая нам лучше понять и сохранить этот уникальный и невероятно важный ресурс нашей планеты.
Вопрос-ответ

Как определить объем в физике без учета массы?
Определение объема в физике без учета массы можно провести с помощью различных методов, таких как метод гидростатического давления, метод архимедовой силы или метод пропускания газа через закрытую систему. Каждый из этих методов подходит для определения объема в зависимости от конкретной ситуации и условий эксперимента.
Каким образом работает метод гидростатического давления для определения объема?
Метод гидростатического давления основан на законе Паскаля, который гласит, что давление, передаваемое жидкостью на границе ее сосуда, распространяется равномерно во всех направлениях. Для определения объема с помощью этого метода необходимо измерить давление, создаваемое жидкостью, и зная другие параметры, такие как плотность жидкости и высота столба жидкости, вычислить объем.
Как применить метод архимедовой силы для определения объема в физике?
Метод архимедовой силы используется для измерения объема тела путем вычисления силы, действующей на тело в жидкости или газе. Для этого необходимо сначала измерить силу, с которой тело толкается вверх, затем, зная плотность среды, в которой находится тело, определить объем. Этот метод основан на законе Архимеда, который утверждает, что тело, погруженное в жидкость или газ, испытывает со стороны среды поддерживающую силу, равную весу вытесненного объема среды.



