Одним из способов построения доверительного интервала является использование формулы Уилсона, которая учитывает как выборочную долю, так и размер выборки. Однако при использовании этой формулы возникает вопрос: строится ли симметричный интервал вокруг оценки? В данной статье мы рассмотрим особенности построения доверительного интервала при оценивании генеральной доли и ответим на этот вопрос.
Генеральная доля: понятие и суть

При оценивании генеральной доли могут использоваться различные методы, такие как точечная оценка, интервальная оценка и другие, чтобы получить более точные и надежные результаты.
Функция доли в статистике
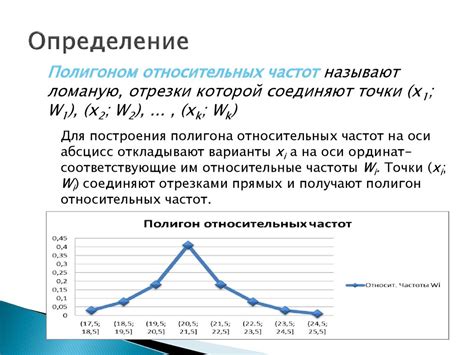
Методы оценивания доли

Оценка доли в генеральной совокупности представляет собой важную задачу статистики. Для этого существуют различные методы, включая:
- Выборочная пропорция: оценка доли на основе данных из выборки. Позволяет получить оценку доли с учетом вариаций в выборке;
- Интервальное оценивание: метод, который предполагает построение доверительного интервала вокруг точечной оценки доли. Позволяет учесть различные возможные значения доли;
- Метод максимального правдоподобия: использование функции правдоподобия для оценки параметров модели, в том числе доли в генеральной совокупности.
Принципы точности оценки доли
При оценке генеральной доли с помощью интервальной оценки важно соблюдать принципы точности, чтобы получить надежные результаты.
- Для построения интервала оценки необходимо определить степень уверенности, которая обычно выражается в виде доверительного уровня, например, 95% или 99%.
- При выборе размера выборки следует учитывать требуемую точность оценки доли и вариабельность данных. Чем больше выборка, тем более точную оценку можно получить.
- При оценке доли следует учитывать симметричность интервала, чтобы минимизировать вероятность ошибки. Для этого используются специальные методы, такие как методы асимптотического построения интервалов.
- Важно также учитывать особенности распределения исследуемой величины, чтобы корректно интерпретировать результаты оценки.
Симметричный интервал: определение и применение
Симметричные интервалы широко используются в статистике для оценки параметров, таких как доли, средние значения и т.д. Они позволяют оценить диапазон значений, в котором с вероятностью определенного уровня (например, 95%) содержится истинное значение параметра.
При оценивании генеральной доли симметричный интервал строится вокруг оценки доли, причем его верхняя и нижняя границы равноудалены от оценки. Такой подход обеспечивает уверенность в том, что истинное значение доли находится в указанном интервале с заданной вероятностью.
Критерии симметричности интервала
При оценивании генеральной доли важно учитывать симметричность интервала оценки. Для определения симметричности интервала можно использовать следующие критерии:
| Критерий | Описание |
|---|---|
| Центральная точка интервала | Интервал оценки должен быть сосредоточен вокруг истинного значения параметра. Центральная точка интервала должна совпадать с оценкой генеральной доли. |
| Равное расстояние от центра | Расстояние от центральной точки интервала до его границ должно быть одинаковым. Это гарантирует симметричность интервала. |
| Симметрия относительно истинного значения | Интервал оценки должен быть симметричен относительно истинного значения параметра. Это обеспечивает сбалансированность оценки. |
Анализ симметричности интервала
Для оценивания генеральной доли часто используется интервальная оценка, которая может быть симметричной или асимметричной. После построения интервала важно проанализировать его симметричность. Симметричный интервал означает, что вероятность того, что оценка генеральной доли лежит выше или ниже точечной оценки, одинакова.
Для анализа симметричности интервала можно проверить разницу между верхней и нижней границами интервала и сравнить её с шириной интервала. Если разница примерно равна половине ширины интервала, то можно считать интервал симметричным.
Симметричные интервалы обычно более надежны и удобны для интерпретации результатов. Однако, если интервал несимметричен, это также может быть информативным признаком о структуре данных и распределении выборки.
Методы проверки симметричности интервала
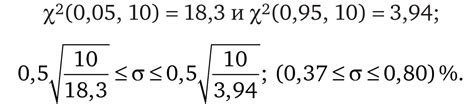
Для оценки симметричности интервала используются различные методы, включая:
| Метод | Описание |
|---|---|
| Метод середины | Проверка, находится ли точка оценки доли в центре интервала. |
| Метод асимметрии | Оценка различия между верхней и нижней границами интервала. |
| Метод медианы | Использование медианы интервала для проверки его центрированности. |
Значение симметричного интервала в статистике

Симметричный интервал строится вокруг точечной оценки параметра и имеет равное расстояние от этой точки в обе стороны. Такой интервал позволяет учесть случайные колебания в данных и дает представление о достоверности оценки.
Важно помнить, что симметричный интервал может иметь различную ширину в зависимости от выбранного уровня доверия. Чем выше уровень доверия, тем шире интервал, так как увеличивается вероятность захвата истинного значения параметра.
Вопрос-ответ

Что такое симметричный интервал при оценивании генеральной доли?
Симметричный интервал при оценивании генеральной доли - это интервал, в котором вероятность того, что истинное значение параметра (генеральной доли) лежит внутри интервала, одинаково распределена относительно среднего значения интервала.
Почему важно строить симметричный интервал при оценивании генеральной доли?
Важно строить симметричный интервал при оценивании генеральной доли, потому что при симметричном интервале с уровнем доверия, равным 95%, есть 95% вероятность того, что истинное значение параметра лежит внутри интервала. Это дает более точное представление о доверительном интервале.
Как строится симметричный интервал при оценивании генеральной доли?
Для построения симметричного интервала при оценивании генеральной доли используются принципы математической статистики и теории доверительных интервалов. Например, при оценке доли процесса в генеральной совокупности можно использовать формулу для расчета интервала с учетом стандартной ошибки.
Как выбор уровня доверия влияет на построение симметричного интервала при оценивании генеральной доли?
Выбор уровня доверия влияет на ширину доверительного интервала. Чем выше уровень доверия, тем шире будет интервал, что означает, что доля процесса будет оценена с большей степенью уверенности, но при этом интервал будет менее точным. Наоборот, при меньшем уровне доверия интервал будет уже, но оценка будет менее надежной.



