Параллельность прямых – одно из основных понятий геометрии, которое имеет множество применений в различных задачах. В стереометрии параллельность прямых также играет важную роль и может быть доказана с помощью определенных принципов и теорем.
Для доказательства параллельности прямых в стереометрии используются различные методы, в том числе геометрические построения и аналитическая геометрия. Важно уметь правильно интерпретировать условия задачи и применять соответствующие приемы для выведения требуемого утверждения.
В данной статье мы рассмотрим основные теоремы и принципы, которые помогут вам доказать параллельность прямых в стереометрии и применить их в разнообразных геометрических задачах.
Аксиома в стереометрии
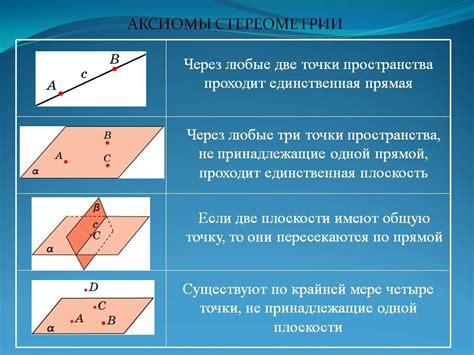
Примером аксиомы в стереометрии может быть утверждение, что через две различные точки можно провести ровно одну прямую.
Определение аксиомы
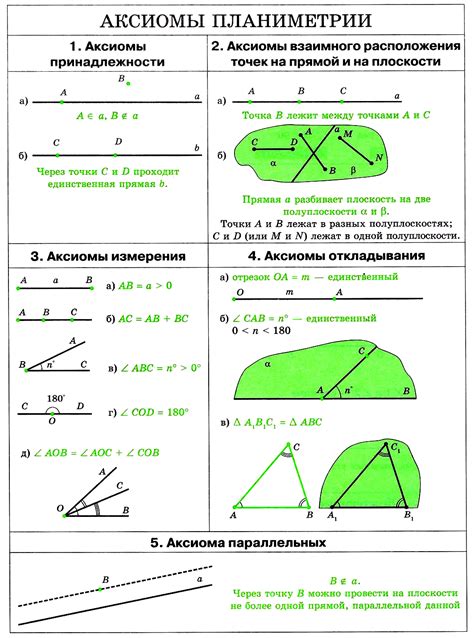
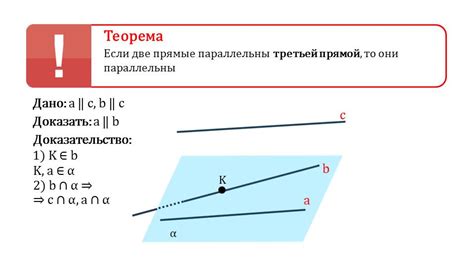
Теорема о параллельных прямых

Если две прямые параллельны третьей прямой, то углы, образуемые этими прямыми с пересекающей и равны между собой.
Дано: две прямые a и b параллельны третьей прямой c.
Требуется: доказать, что углы α и β равны.
- Проведем перпендикуляр k к прямым a и b из точки пересечения прямых a и c.
- Прямая k пересекает прямую b в точке D.
- В треугольнике ADC углы α и γ являются вертикальными, а значит, α = γ.
- В треугольнике CDB углы β и γ являются вертикальными, а значит, β = γ.
- Из пунктов 3 и 4 следует, что α = β.
Доказательство теоремы
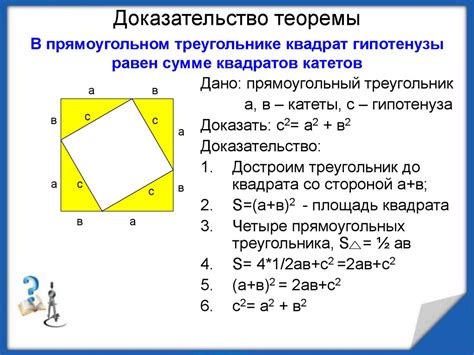
Для доказательства параллельности прямых в стереометрии, мы можем воспользоваться критерием параллельности двух прямых, идущих в плоскостях, параллельных данным плоскостям.
Пусть у нас имеются две параллельные плоскости α и β, а также прямая l, лежащая в плоскости α, и прямая m, лежащая в плоскости β. Предположим, что прямые l и m пересекаются в точке A. Тогда проведем две плоскости, одна проходящая через прямую l и параллельная плоскости β, а другая проходящая через прямую m и параллельная плоскости α.
| Точка | Плоскость |
| A | l |
| A | m |
Таким образом, мы получаем, что прямые l и m должны быть параллельными, так как они лежат в параллельных плоскостях.
Аксиома параллельности
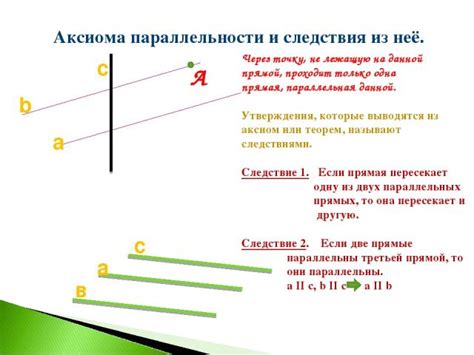
Согласно данной аксиоме, параллельные прямые не пересекаются ни в одной точке пространства. Используя это свойство, можно подтверждать или опровергать параллельность прямых и выполнять различные геометрические доказательства.
| Значение | Аксиома параллельности |
| Утверждение | Через точку, не принадлежащую данной прямой, существует только одна прямая, параллельная данной. |
| Применение | Используется для построения геометрических конструкций и доказательств в стереометрии. |
Применение в практике

Применение доказательства параллельности прямых позволяет точно определить взаимное расположение элементов трехмерной геометрии, определить углы между плоскостями и прямыми, а также обнаружить сходство или различие между фигурами.
- Параллельные прямые могут быть использованы в построении прямоугольных параллелепипедов, треугольников и других геометрических фигур.
- С помощью данного доказательства можно проверить и уточнить решения задач, связанных с расположением плоскостей и прямых в пространстве, что делает его полезным инструментом для инженеров, дизайнеров и архитекторов.
Метод поиска параллельности
| Если две прямые параллельны, то соответствующие углы равны |
| Если две прямые пересекаются, то соответствующие углы не равны |
| Используя данное условие, можно провести соответствующие измерения углов на сторонах, где прямые пересекаются, и сравнить их. |
Точность измерений
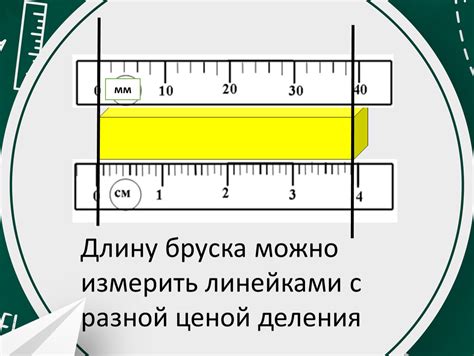
При доказательстве параллельности прямых в стереометрии необходимо обращать внимание на точность измерений. Даже малейшая погрешность может привести к неверному результату. Поэтому важно использовать точные инструменты и методы измерения, а также учитывать условия проведения эксперимента.
Особое внимание следует уделить правильной установке инструментов и исключению случайных ошибок. Повторяемость измерений и проверка результатов помогут обеспечить достоверность полученных данных.
Вопрос-ответ

Как можно доказать параллельность двух прямых в стереометрии?
Для доказательства параллельности двух прямых в стереометрии можно использовать несколько способов. Один из основных способов - это показать, что углы между этими прямыми равны. Это можно сделать, например, если прямые пересекаются с третьей прямой, и углы при пересечении равны. Также параллельность можно доказать, если две прямые параллельны одной и той же плоскости, либо если они параллельны плоскостям, перпендикулярным друг другу.
Какие свойства прямых используются для доказательства их параллельности в стереометрии?
Для доказательства параллельности прямых в стереометрии можно использовать свойства параллельных прямых, такие как равные углы при пересечении двух параллельных прямых третьей прямой, а также свойства параллельных плоскостей, например, если две прямые перпендикулярны к одной и той же плоскости и параллельны друг другу. Также можно применять свойства перпендикулярных прямых и плоскостей.
Можно ли доказать параллельность прямых, не зная углов между ними?
Да, параллельность двух прямых можно доказать и без знания углов между ними. Например, если данные прямые пересекаются с третьей прямой и углы при пересечении равны, то можно сделать вывод о параллельности данных прямых. Также можно воспользоваться свойствами параллельных прямых и плоскостей для доказательства параллельности прямых без известных углов.
Какие принципы геометрии используются для доказательства параллельности прямых в стереометрии?
Для доказательства параллельности прямых в стереометрии используются принципы геометрии, такие как свойства параллельных прямых и плоскостей, теоремы о перпендикулярных прямых и плоскостях, правила равенства углов при пересечении прямых и плоскостей. Также для доказательства параллельности прямых можно применять теоремы о соответствующих, вертикальных и других углах.
Как можно доказать параллельность двух прямых в стереометрии?
Для доказательства параллельности двух прямых в стереометрии можно использовать несколько методов. Один из наиболее распространенных способов - это использование векторного анализа. Если векторы, задающие данные прямые, коллинеарны (или пропорциональны), то прямые параллельны. Еще один способ - это использование свойств параллельных прямых в пространстве, например, если две прямые пересекаются с третьей под углами, равными внутренним или внешним углам между параллельными прямыми, то они также параллельны. Для доказательства параллельности прямых важно отталкиваться от свойств геометрических фигур и их взаимного расположения в пространстве.



