Пересечение прямых в плоскости – одно из фундаментальных понятий геометрии, которое находит широкое применение в математике и ее прикладных областях. Понимание того, как и почему прямые в плоскости пересекаются, позволяет нам решать различные задачи и строить сложные конструкции.
Существует несколько способов доказательства пересечения прямых в плоскости. Один из наиболее простых и эффективных методов – это использование аксиом и свойств плоскости, которые позволяют установить факт пересечения двух прямых в определенной точке.
При рассмотрении доказательства пересечения прямых в плоскости важно помнить об основных геометрических принципах и используемых теоремах, которые позволяют нам объяснить и обосновать этот феномен. Данный математический факт является основой многих теорем и задач в геометрии, а также находит свое применение в решении практических задач.
Метод проекций вектора
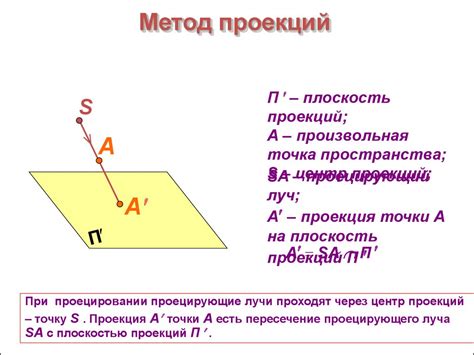
Для того чтобы применить этот метод, необходимо определить векторы, которые задают данные прямые, а затем рассмотреть их проекции на оси. Если проекции не совпадают, то прямые пересекаются в указанной точке. В случае если проекции совпадают, прямые либо параллельны, либо совпадают.
Метод проекций вектора позволяет быстро и наглядно определить взаимное расположение прямых на плоскости и является одним из важных инструментов геометрии.
Теорема о пересечении прямых в координатах
Пусть заданы две прямые в пространстве: y = k1x + b1 и y = k2x + b2. Тогда эти прямые пересекаются в точке с координатами:
- x = (b2 - b1) / (k1 - k2)
- y = k1((b2 - b1) / (k1 - k2)) + b1
Если коэффициенты k1 и k2 прямых равны, то прямые параллельны и не пересекаются.
Геометрическое понимание пересечения прямых
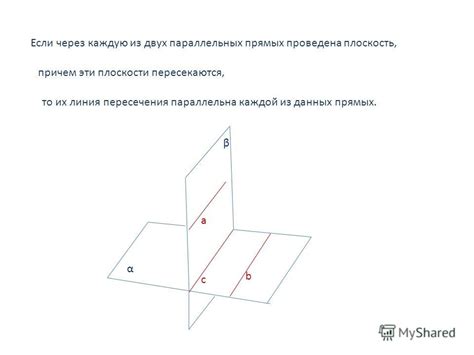
Геометрическое понимание пересечения прямых позволяет анализировать их взаимное положение и строить различные геометрические построения. При изучении прямых важно учитывать их угловые и длинные характеристики, такие как наклон, расстояние между прямыми и их пересечение с осями координат.
Использование системы уравнений для доказательства

Понятие угла между прямыми

Угол между двумя прямыми в плоскости определяется как угол между направляющими векторами этих прямых. Если прямые заданы уравнениями вида ax + by + c = 0, то направляющие вектора можно найти как нормализованные коэффициенты перед переменными x и y.
Угол между двумя прямыми можно найти с помощью формулы:
- Найдите направляющие вектора для каждой из прямых.
- Найдите угол между направляющими векторами с помощью формулы для угла между векторами.
Угол между прямыми может быть острый (менее 90 градусов), прямой (равен 90 градусов) или тупой (более 90 градусов). Это понятие играет важную роль при изучении пересечения прямых в плоскости.
Проективное доказательство пересечения

В геометрии проективные преобразования играют важную роль при рассмотрении пересечения прямых в плоскости. Проективное доказательство пересечения прямых основано на принципе сохранения пересечения при проективных преобразованиях.
Для доказательства пересечения прямых проективным методом рассматривается специальное проективное преобразование, которое переводит данные прямые в прямые, пересекающиеся в точке на бесконечности. Это позволяет утверждать, что исходные прямые тоже пересекаются в точке, что и требовалось доказать.
Прямые параллельны
Если коэффициенты наклона двух прямых равны и их угловые коэффициенты совпадают, то мы имеем дело с параллельными прямыми. В этом случае прямые не пересекаются и не имеют общих точек на плоскости.
Обобщение понятия пересечения прямых на плоскости

При рассмотрении пересечения прямых на плоскости, важную роль играют различные варианты их взаимного расположения. Для двух прямых существует несколько возможных случаев пересечения:
| В случае, если две прямые пересекаются точкой, расположенной вне обоих линий; |
| Прямые могут касаться друг друга лишь в одной точке, в этом случае они называются касательными; |
| Также может возникнуть ситуация, когда прямые совпадают и пересекаются бесконечным количеством точек, образуя одну и ту же прямую; |
| В случае параллельных прямых, они не пересекаются ни в одной точке и всегда остаются друг от друга на постоянном расстоянии; |
| Если две прямые лежат на одной плоскости и не пересекаются, они называются некоординатно или всего лишь несовместны. |
Вопрос-ответ

Как доказать пересечение двух прямых в плоскости?
Для доказательства пересечения двух прямых в плоскости обычно используют метод решения системы уравнений, задающих прямые. Если две прямые заданы уравнениями вида y = k1*x + b1 и y = k2*x + b2, где k1, k2 - наклоны прямых, а b1, b2 - их свободные члены, то пересечение найдется путем решения системы уравнений k1*x + b1 = k2*x + b2 для x и y. Если при решении системы нашлось решение, то прямые пересекаются, если нет - прямые параллельны.
Какие бывают случаи пересечения прямых в плоскости?
Существует три варианта взаимного расположения двух прямых в плоскости: прямые пересекаются в одной точке (то есть имеют одну общую точку), прямые параллельны (не имеют общих точек) или прямые совпадают. Для каждого случая существует свой способ и критерий доказательства пересечения или непересечения прямых.
Можно ли доказать пересечение прямых без использования уравнений?
Да, можно доказать пересечение прямых в плоскости и другими способами, например, с помощью геометрических построений. Если построить две прямые на координатной плоскости и убедиться, что они не параллельны, то пересечение будет очевидно. Однако для точного доказательства пересечения или непересечения прямых, уравнения часто предпочтительнее использовать.



