Шар – геометрическое тело, каждая точка которого находится на одинаковом расстоянии от его центра. Произвольный шар можно описать всего одним параметром – радиусом: это расстояние от центра шара до его поверхности.
Вычисление радиуса шара является одной из базовых задач геометрии, и эту задачу можно решить несколькими способами. Один из наиболее простых способов – использование формулы для объема шара и подставление известных значений.
Давайте рассмотрим несколько методов, которые помогут нам определить радиус шара в различных ситуациях.
Как вычислить радиус
Для вычисления радиуса шара можно воспользоваться формулой из геометрии. Радиус шара представляет собой расстояние от его центра до любой точки поверхности.
Используя формулу для объема шара, радиус можно найти по следующему уравнению:
r = ∛(3V)/(4π)
Где r - радиус шара, V - объем шара, π - число Пи (примерное значение 3.14159). Для вычисления радиуса шара необходимо знать его объем. После нахождения объема, можно подставить значения в формулу и получить радиус.
Метод через диаметр
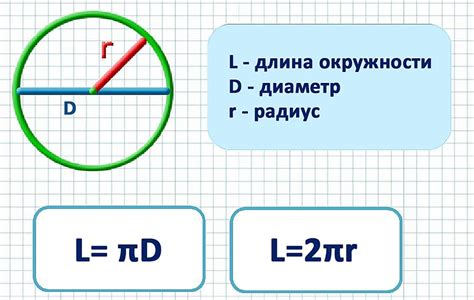
Для вычисления радиуса шара можно воспользоваться диаметром, который представляет собой отрезок, соединяющий две противоположные точки на поверхности шара через его центр.
Для нахождения радиуса шара по диаметру необходимо разделить диаметр на 2, так как радиус равен половине диаметра. Таким образом, чтобы найти радиус по диаметру, необходимо просто поделить значение диаметра на 2.
Формула для вычисления радиуса шара через диаметр: радиус = диаметр / 2.
Формула через объем
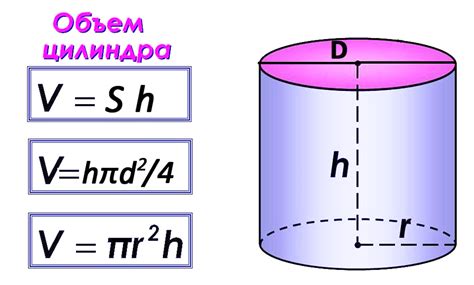
Радиус шара (r) = √(3V / (4π))
Где V - объем шара, а π - математическая константа, примерно равная 3.14159.
Вычисление радиуса шара через площадь поверхности
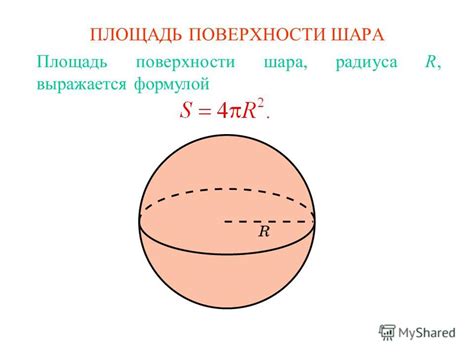
Для вычисления радиуса шара через его площадь поверхности можно воспользоваться формулой:
| Радиус шара (r) = √(Площадь поверхности / 4π) |
Где π (пи) - математическая константа, приблизительно равная 3.14159. Чтобы вычислить радиус шара, необходимо знать его площадь поверхности и подставить значения в указанную формулу.
Анализ способов нахождения радиуса
Существует несколько способов определения радиуса шара: через длину окружности или площадь поверхности шара, а также через объем шара.
1. Радиус через длину окружности: Для нахождения радиуса можно использовать формулу r = l / (2π), где l - длина окружности.
2. Радиус через площадь поверхности: Для этого можно воспользоваться формулой r = √(S / 4π), где S - площадь поверхности шара.
3. Радиус через объем шара: Если известен объем шара, то радиус можно найти по формуле r = √(3V / 4π), где V - объем шара.
Вопрос-ответ

Какой способ применяется для вычисления радиуса шара по его объему?
Для вычисления радиуса шара по его объему используется формула: \( r = \sqrt[3]{\frac{3V}{4\pi}} \), где \( r \) - радиус шара, \( V \) - его объем, а \( \pi \) - число Пи, приблизительно равное 3.14159. Эта формула выводится из формулы для объема шара \( V = \frac{4}{3} \pi r^3 \).
Как можно вычислить радиус шара по его площади поверхности?
Для вычисления радиуса шара по площади его поверхности можно воспользоваться формулой: \( r = \sqrt{\frac{S}{4\pi}} \), где \( r \) - радиус шара, а \( S \) - площадь его поверхности. Эта формула выводится из формулы для площади поверхности шара \( S = 4\pi r^2 \), разрешая уравнение относительно радиуса.



