Арифметическая и геометрическая прогрессии являются основными понятиями алгебры и анализа. Несмотря на то, что обе они представляют собой последовательности чисел, их основные принципы отличаются друг от друга.
Арифметическая прогрессия характеризуется постоянным разностью между соседними членами последовательности, в то время как в геометрической прогрессии каждый последующий член получается умножением предыдущего на некоторый фиксированный множитель.
Основные различия между этими двумя видами прогрессий заключаются в способе образования и изменении элементов в последовательности, что имеет существенное значение при решении различных задач и уравнений.
Основные различия между арифметической и геометрической прогрессиями

Вот ключевые различия между арифметической и геометрической прогрессиями:
- В арифметической прогрессии разница между любыми двумя последовательными членами постоянна, тогда как в геометрической прогрессии члены увеличиваются или уменьшаются в соответствии с постоянным множителем.
- Арифметическая прогрессия имеет вид: a, a+d, a+2d, a+3d, ..., где 'a' - начальный член, 'd' - разность, в то время как геометрическая прогрессия представляется как: a, ar, ar^2, ar^3, ..., где 'a' - начальный член, 'r' - множитель.
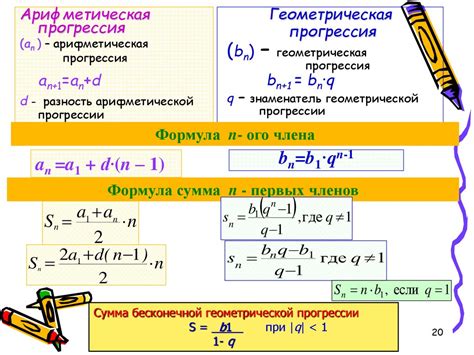
- Сумма n членов арифметической прогрессии можно выразить формулой Sn = n/2 * (2a + (n-1)d), а для геометрической прогрессии формула для суммы n членов будет Sn = a*(r^n - 1)/(r - 1).
- В обоих прогрессиях можно найти n-й член, используя формулы: для АП an = a + (n-1)d и для ГП an = a * r^(n-1).
Определение арифметической прогрессии

Общий вид арифметической прогрессии: an = a1 + (n-1)d, где an – n-й член прогрессии, a1 – первый член прогрессии, d – разность арифметической прогрессии, n – номер члена прогрессии.
Определение геометрической прогрессии

Например, если задана геометрическая прогрессия с первым членом 2 и знаменателем 3, то члены прогрессии будут: 2, 6, 18, 54 и т.д., так как каждый следующий член равен предыдущему, умноженному на 3.
Структура арифметической прогрессии

Арифметическая прогрессия (АП) представляет собой последовательность чисел, в которой каждый следующий элемент отличается от предыдущего на постоянную величину, называемую шагом (d). Для вычисления любого элемента арифметической прогрессии используется формула:
an = a1 + (n-1) * d,
где an - n-й член прогрессии, a1 - первый член прогрессии, n - номер члена прогрессии, d - шаг прогрессии.
Таким образом, структура арифметической прогрессии определяется постоянным шагом, который позволяет определить любой элемент последовательности, зная только первый член и номер элемента.
Структура геометрической прогрессии
Геометрическая прогрессия представляет собой ряд чисел, где каждый последующий элемент получается умножением предыдущего на определенное число, называемое знаменателем геометрической прогрессии.
Общая формула n-го члена геометрической прогрессии выглядит следующим образом:
an = a1 * qn-1,
где:
- an - n-й член прогрессии
- a1 - первый член прогрессии
- q - знаменатель прогрессии
- n - номер члена прогрессии
Таким образом, структура геометрической прогрессии определяется рекуррентным соотношением, которое позволяет находить любой член последовательности по известным начальным условиям.
Формула общего члена арифметической прогрессии

Арифметическая прогрессия характеризуется тем, что разность между любыми двумя последовательными членами постоянна. Общий член арифметической прогрессии можно выразить следующей формулой:
an = a1 + (n-1)d,
где:
an - n-ый член прогрессии,
a1 - первый член прогрессии,
d - разность между членами прогрессии,
n - номер члена прогрессии.
Формула общего члена геометрической прогрессии

Общий член геометрической прогрессии вычисляется по формуле:
$$a_n = a_1 \cdot q^{n-1}$$
Где:
- $$a_n$$ - n-й член последовательности;
- $$a_1$$ - первый член последовательности;
- $$q$$ - множитель прогрессии, также называемый знаменателем.
Эта формула позволяет легко находить любой член геометрической прогрессии, зная лишь первый член и множитель прогрессии.
Практическое применение арифметической и геометрической прогрессий

Арифметическая прогрессия:
Арифметическая прогрессия широко применяется в финансовых расчетах, планировании бюджета и в задачах по определению средних значений. Например, если известен первый член прогрессии (начальный капитал), разность и количество членов, можно легко определить сумму всех членов прогрессии, что позволяет эффективно управлять финансами.
Геометрическая прогрессия:
Геометрическая прогрессия находит свое применение в задачах, где рост или уменьшение величин происходит не постепенно, а с определенным множителем. Например, она часто используется в экономике для моделирования экспоненциального роста или убывания индексов, а также в задачах, связанных с прогнозированием темпов развития процессов.
Вопрос-ответ

Какие основные отличия между арифметической и геометрической прогрессиями?
Основное различие между арифметической и геометрической прогрессиями заключается в том, как изменяются элементы последовательности. В арифметической прогрессии каждый следующий элемент получается путем добавления к предыдущему одного и того же числа (шага), когда в геометрической прогрессии каждый следующий элемент получается путем умножения предыдущего элемента на одно и то же число (знаменатель). Также отличаются формулы для общего члена и суммы элементов прогрессии.
В чем заключается главное сходство между арифметической и геометрической прогрессиями?
Основное сходство между арифметической и геометрической прогрессиями заключается в том, что в обоих случаях мы имеем последовательность чисел, которые имеют определенные закономерности в изменении между собой. То есть в обеих прогрессиях каждый новый элемент зависит от предыдущего и задается определенным правилом. Это делает их одними из основных и наиболее изучаемых типов числовых последовательностей.
Какие примеры можно привести арифметической и геометрической прогрессии в повседневной жизни?
Примером арифметической прогрессии в повседневной жизни может служить увеличение заработной платы сотрудника каждый год на фиксированную сумму. Например, если в первый год он получает 1000 долларов, во второй - 1100 долларов и так далее, то это арифметическая прогрессия. Примером геометрической прогрессии может быть увеличение в размере геометрической прогрессии каждый год, например, если урожайность поля увеличивается в 2 раза от года к году.
В чем состоит основное практическое применение арифметической и геометрической прогрессий?
Арифметическая прогрессия широко используется в учебных задачах, экономике (например, при расчете аннуитетов, росте доходов), физике (при описании движения с постоянным ускорением) и в других областях, где важна линейная зависимость между элементами последовательности. Геометрическую прогрессию можно встретить, например, при расчете процентов, при удвоении суммы инвестиций через определенное количество периодов, в задачах о популяции и развитии биологических процессов.



