Скалярное и векторное произведение векторов – фундаментальные понятия линейной алгебры, играющие важную роль в математике и физике. Оба вида произведений позволяют производить операции над векторами, но имеют разные свойства и применение в различных сферах.
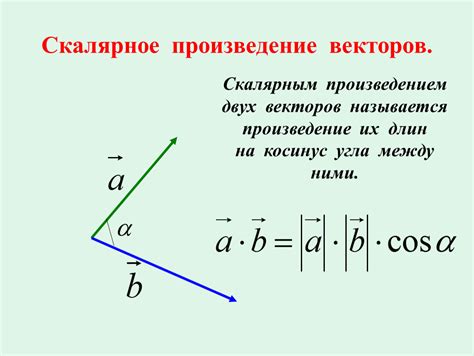
Скалярное произведение векторов – это операция, результатом которой является число (скаляр). Оно определяет угол между векторами и используется, например, для вычисления проекции одного вектора на другой, а также для определения длины вектора.
Векторное произведение векторов – это операция, результатом которой является вектор. Оно позволяет вычислить вектор, перпендикулярный плоскости, образованной двумя исходными векторами, и находит широкое применение, например, в механике и электродинамике.
Скалярное произведение векторов: определение и свойства

Скалярное произведение обладает следующими свойствами:
1. Коммутативность: $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
2. Дистрибутивность по сложению: $(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}$
3. Умножение на скаляр: $(k \cdot \vec{a}) \cdot \vec{b} = k \cdot (\vec{a} \cdot \vec{b})$
С помощью скалярного произведения можно определять угол между векторами, расстояния между точками, а также проекции векторов на другие вектора.
Скалярное умножение векторов: формула и примеры
Формула: \( \overrightarrow{a} \cdot \overrightarrow{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z \), где \( a_x, a_y, a_z \) и \( b_x, b_y, b_z \) – координаты соответствующих векторов по осям \( x, y \) и \( z \).
Пример скалярного умножения векторов \( \overrightarrow{a} \) и \( \overrightarrow{b} \):
Пусть \( \overrightarrow{a} = (3, -2, 5) \) и \( \overrightarrow{b} = (1, 4, -1) \).
Тогда \( \overrightarrow{a} \cdot \overrightarrow{b} = 3 \cdot 1 + (-2) \cdot 4 + 5 \cdot (-1) = 3 - 8 - 5 = -10 \).
Векторное произведение векторов: особенности и применение
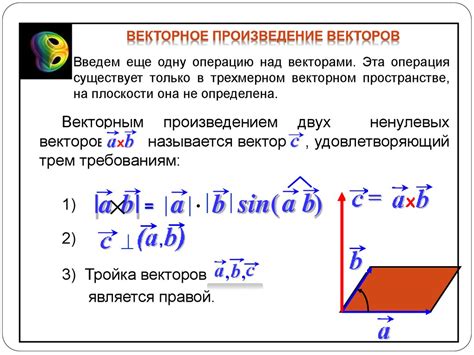
Применение векторного произведения широко распространено в физике, математике, геометрии и технике. Например, векторное произведение часто используется при вычислении момента силы относительно определенной точки, при нахождении площади треугольника, построении прямой по двум точкам и многих других задачах.
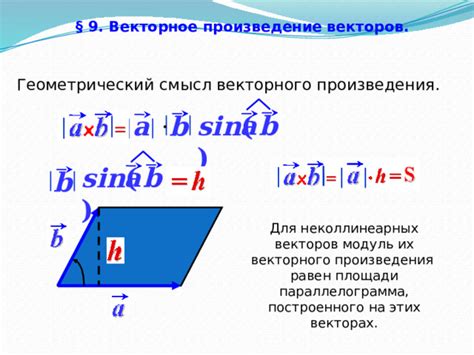
Векторное умножение векторов: правило и геометрический смысл
Правило векторного умножения векторов можно записать следующим образом. Пусть даны два вектора a и b, тогда их векторное произведение обозначается как a x b и вычисляется по следующей формуле:
| a x b = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1) |
Геометрический смысл этой операции заключается в получении вектора, перпендикулярного к плоскости, образованной исходными векторами, и его направление определяется с помощью правила буравчика. Векторное умножение используется во многих областях физики и математики, например, для нахождения момента силы относительно заданной точки или для определения ориентации трехмерных объектов.
Применение скалярного и векторного произведения в физике и геометрии

Скалярное произведение используется, например, при расчетах силы, совершаемой телом под действием внешних сил, а также при определении угла между векторами и проекций одного вектора на другой.
Векторное произведение, в свою очередь, позволяет находить векторную характеристику векторов, например, момент силы, угловую скорость и т.д. Оно также используется для определения площади параллелограмма, построенного на двух векторах, и определения нормали к плоскости, в которой лежат векторы.
Вопрос-ответ

В чем различие между скалярным и векторным произведением векторов?
Скалярное произведение векторов – это операция, результатом которой является число, значение которого равно произведению модулей векторов на косинус угла между ними. Векторное произведение же даёт новый вектор, перпендикулярный плоскости, образованной первыми двумя векторами. Таким образом, основное различие заключается в том, что скалярное произведение возвращает число, а векторное – вектор.
В каких ситуациях используются скалярное и векторное произведения векторов?
Скалярное произведение векторов применяется, например, для нахождения угла между двумя векторами, проверки ортогональности векторов, вычисления проекции одного вектора на другой и решения различных физических задач. Векторное же произведение используется при определении площади параллелограмма, построении прямой или плоскости по заданным векторам, вычислении момента силы относительно точки и других задачах, требующих определения нового вектора, перпендикулярного двум другим.



