Треугольник – одна из фундаментальных геометрических фигур, изучаемых с древних времен. Вокруг треугольников сложено множество теорем и свойств, которые помогают понять их характеристики и взаимосвязи.
Биссектриса – линия, делящая угол на две равные части. В геометрии существуют различные типы биссектрис, включая биссектрисы углов и биссектрисы сторон треугольника. Но существует ли треугольник, у которого биссектрисы каждого угла перпендикулярны друг другу?
Исследование треугольника с перпендикулярными биссектрисами

Предположим, что у нас есть треугольник ABC с перпендикулярными биссектрисами. Это означает, что точки пересечения биссектрис с противоположными сторонами треугольника будут лежать на одной прямой и будут образовывать прямой угол.
Для такого треугольника справедливо следующее утверждение: если из точек пересечения биссектрис с противоположными сторонами провести отрезки до вершин треугольника, то эти отрезки будут равными и пересекутся в центре окружности, вписанной в треугольник ABC.
Таким образом, треугольник с перпендикулярными биссектрисами обладает некоторыми интересными геометрическими свойствами, которые могут быть использованы при решении учебных задач.
Теорема о существовании

Другими словами, заданные условия могут быть выполнены, и такой треугольник существует.
Доказательство теоремы
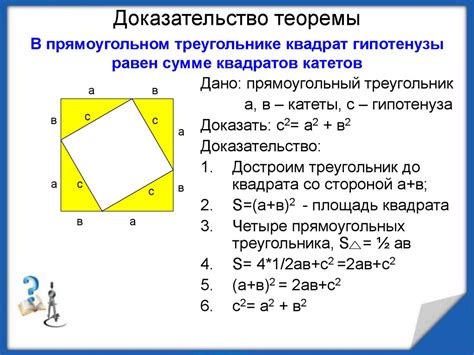
- Пусть у треугольника ABC перпендикуляры к биссектрисам проведены из точек A, B и C, и пересекаются в точке O.
- Пусть D и E – середины сторон AC и AB соответственно.
- Так как OD перпендикулярен AB и OC перпендикулярен AB, то ODOC – прямоугольник. Аналогично получаем, что ODOB – прямоугольник.
- Так как OD = OC и OD // AB, то OC // AB.
- Аналогично доказывается, что OB // AC и OA // BC.
- Отсюда следует, что треугольник ABC – равнобедренный: AB = AC, BC = AC, AC = BC.
Геометрическое представление
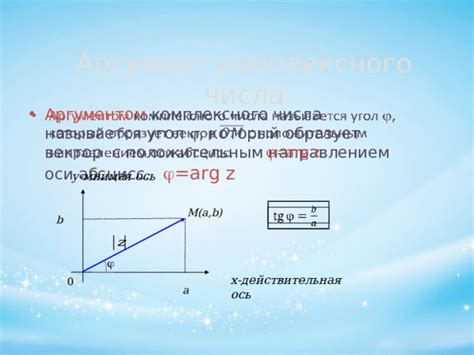
Теперь обратим внимание на треугольники ADB и ADC. В этих треугольниках углы ADB и ADC равны, а угол BDA общий. Поэтому треугольники совпадают по двум сторонам и углу между ними. То же самое можно сказать и про треугольники BEC и BED, а также CFD и CFE. Значит, треугольник ABC равнобедренный, а его биссектрисы действительно перпендикулярны.
Пример построения треугольника с перпендикулярными биссектрисами

Построим треугольник ABC с перпендикулярными биссектрисами.
1. Начнем с построения отрезков AB и AC любой длины.
2. Найдем точку D на отрезке AB, которая на равном расстоянии от точек A и B, так что AD = BD.
3. Рассмотрим отрезок DC и найдем точку E на нем такую, что CE = CD, а угол CDE равен 90 градусов.
4. Точка E будет вершиной треугольника с перпендикулярными биссектрисами, так как CE - биссектриса угла ACB, а DE - биссектриса угла ADC.
Таким образом, треугольник CDE будет иметь перпендикулярные биссектрисы в вершине C, что подтверждает возможность построения треугольника с перпендикулярными биссектрисами.
Практическое применение

Треугольник с перпендикулярными биссектрисами имеет ряд свойств, которые могут быть использованы в различных практических задачах.
Например, такой треугольник может быть использован в геодезии для измерения углов и расстояний. Перпендикулярность биссектрис позволяет точно определять положение объектов на местности и проводить точные замеры.
Также треугольник с перпендикулярными биссектрисами используется в архитектуре и строительстве при построении перегородок и установке предметов под определенными углами.
Вопрос-ответ

Может ли треугольник иметь перпендикулярные биссектрисы?
Да, существуют треугольники, у которых биссектрисы перпендикулярны друг другу. Такие треугольники называются прямоугольными треугольниками.
Как можно определить, что биссектрисы треугольника являются перпендикулярными друг другу?
Биссектрисы треугольника будут перпендикулярными друг другу, если треугольник является прямоугольным, то есть угол между биссектрисами будет 90 градусов.
Есть ли способ построить треугольник с перпендикулярными биссектрисами?
Да, можно построить прямоугольный треугольник, где угол между катетами будет 90 градусов, а биссектрисы, проведенные из вершин прямого угла, будут перпендикулярными друг другу.
Какие свойства имеют треугольники с перпендикулярными биссектрисами?
Треугольники с перпендикулярными биссектрисами являются прямоугольными. Они обладают уникальными характеристиками, такими как равенство катетов и другие закономерности, связанные с прямоугольными треугольниками.



