Смешанное произведение векторов – это одно из базовых понятий линейной алгебры, которое применяется в геометрии и физике. Оно позволяет определить объем параллелепипеда, образованного тремя векторами, а также найти направление вектора, перпендикулярного данной плоскости. Но вопрос о знаке смешанного произведения часто вызывает недопонимание: должен ли он быть положительным или отрицательным?
Смешанное произведение векторов определяется как векторное произведение одного вектора на векторное произведение двух других: очень важно при этом помнить о порядке следования векторов, поскольку смена порядка меняет знак результата. Если смешанное произведение положительно, то векторы совместно ориентированы, в противном случае – противоположно.
Исследуя свойства и приложения смешанного произведения векторов, мы можем найти много интересных задач, позволяющих лучше понять его роль в математике и физике. Изучение этого понятия поможет углубить знания в векторной алгебре и применить их на практике в различных областях науки.
Смешанное произведение векторов: определение и свойства

Основные свойства смешанного произведения векторов:
- Смешанное произведение векторов не зависит от порядка векторов: \( \vec{a} \cdot (\vec{b} \times \vec{c}) = \vec{b} \cdot (\vec{c} \times \vec{a}) = \vec{c} \cdot (\vec{a} \times \vec{b}) \).
- Смешанное произведение векторов может быть представлено в виде определителя матрицы из координат векторов.
- Значение смешанного произведения векторов равно объему параллелепипеда, построенного на векторах \( \vec{a} \), \( \vec{b} \) и \( \vec{c} \), учитывая знак в зависимости от ориентации параллелепипеда.
Смешанное произведение векторов: формула и расчет
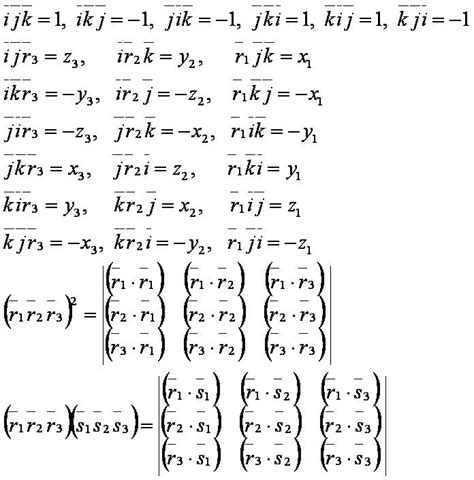
Смешанное произведение векторов играет важную роль в линейной алгебре и геометрии. Формула для смешанного произведения трех векторов в трехмерном пространстве выглядит следующим образом:
| (a x b) • c = a • (b x c) = b • (c x a) |
Где a, b, c - три вектора. Для вычисления смешанного произведения достаточно вычислить определитель матрицы, составленной из координат векторов:
| (a x b) • c = det([a, b, c]) |
Расчет смешанного произведения векторов часто используется при работе с объемами параллелепипедов и определении взаимного расположения векторов в пространстве. Правильное вычисление этой операции позволяет эффективнее работать с векторами и решать геометрические задачи.
Геометрический смысл смешанного произведения векторов
Смешанное произведение векторов представляет собой объём параллелепипеда, построенного на этих векторах. Поэтому, знак смешанного произведения позволяет определить ориентацию построенного объёма.
Положительное смешанное произведение векторов указывает на то, что векторы образуют правую тройку, то есть при их расположении по порядку: первый вектор, второй вектор, третий вектор образуют правую руковую систему координат.
Например: Если векторы A, B и C образуют правую тройку, то значение смешанного произведения будет положительным.
Отрицательное смешанное произведение указывает на обратную ориентацию векторов, то есть на образование левой тройки.
Например: Если векторы A, B и C образуют левую тройку, то значение смешанного произведения будет отрицательным.
Смешанное произведение векторов: примеры и задачи

Пример 1: Найти объем параллелепипеда, построенного на векторах a, b, c.
Решение: Для подсчета объема параллелепипеда нужно вычислить модуль смешанного произведения векторов a, b, c.
Пример 2: Проверить, пересекаются ли векторы a, b, c в одной плоскости.
Решение: Если смешанное произведение равно нулю, то векторы лежат в одной плоскости. В противном случае – нет.
Пример 3: Найти площадь параллелограмма, построенного на векторах a, b.
Решение: Модуль смешанного произведения a, b представляет собой площадь параллелограмма, противолежащего отрезку, образованному векторами a и b.
Смешанное произведение векторов: значимость в математике и физике

В математике смешанное произведение векторов играет важную роль при решении геометрических задач, таких как определение объемов тел, площадей поверхностей и углов между векторами. Оно также используется в курсе линейной алгебры для вычисления детерминанта матрицы и решения систем линейных уравнений.
В физике смешанное произведение векторов применяется для описания момента силы, крутящего момента и других векторных величин, связанных с движением тела в пространстве. Это позволяет ученым моделировать и предсказывать поведение физических систем, а также применять законы сохранения энергии и момента импульса.
Смешанное произведение векторов: связь с объемом параллелепипеда
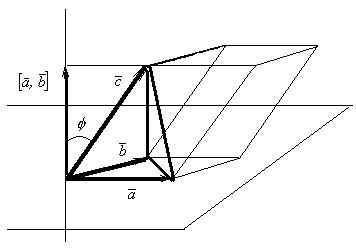
Смешанное произведение векторов представляет собой алгебраическую операцию, которая используется для определения объема параллелепипеда, построенного на данных векторах. Смешанное произведение может быть выражено как скалярное произведение одного вектора на векторное произведение двух других векторов.
Связь смешанного произведения с объемом параллелепипеда проявляется в том, что модуль смешанного произведения векторов равен объему параллелепипеда, образованного этими векторами. Знак смешанного произведения указывает на направление объема параллелепипеда - отрицательное значение соответствует объему, направленному в противоположную сторону.
Смешанное произведение векторов: положительный и отрицательный знак

Смешанное произведение векторов может быть положительным или отрицательным в зависимости от положения векторов относительно друг друга. Если объемный угол между векторами задается правилом правой руки, то смешанное произведение будет положительным. В случае, если угол задается левой рукой, то знак смешанного произведения будет отрицательным. Это связано с правилом ориентации пространства и систем координат.
Смешанное произведение векторов: применение в линейной алгебре

Одним из основных свойств смешанного произведения является то, что его знак зависит от ориентации векторов. Если векторы образуют правую тройку, то знак смешанного произведения будет положительным, а если образуют левую тройку – отрицательным.
Применение смешанного произведения в линейной алгебре позволяет вычислять объемы параллелепипедов, определять ориентацию поверхностей и многое другое. Это помогает решать задачи аналитической и геометрической природы, а также углублять понимание пространственных отношений между векторами.
Формула для вычисления объема тетраэдра
Смешанное произведение векторов представляет собой число, равное объему параллелепипеда, построенного на этих векторах. Для тетраэдра, образованного четырьмя векторами a, b, c и d, смешанное произведение определяется тремя векторами, например,
V = a * (b x c) или V = a * b * c, где x обозначает векторное произведение.
Формула для вычисления объема тетраэдра через смешанное произведение векторов выглядит следующим образом:
V = a * (b x c) = a * b * c = - a * c * b = - (a x b) * c = - (a x c) * b
Эта формула позволяет найти объем тетраэдра, заданного четырьмя векторами, используя смешанное произведение векторов. Познание этого понятия является важным для решения задач геометрии и линейной алгебры.
Смешанное произведение векторов: связь с ориентированным объемом фигур
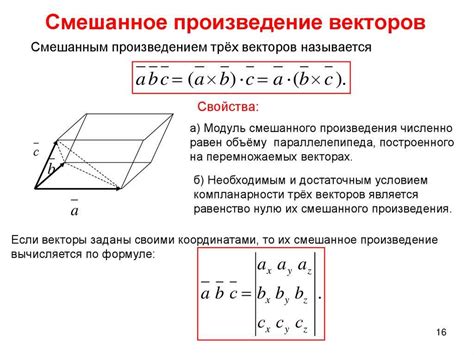
Смешанное произведение векторов имеет важное геометрическое значение, так как оно связано с ориентированным объемом параллелепипеда, образованного этими векторами. Если смешанное произведение векторов положительное, то объем фигуры, образованной этими векторами, положителен, что означает, что векторы образуют правую тройку. Если же смешанное произведение отрицательное, то объем фигуры будет отрицательным, что соответствует образованию левой тройки векторов.
Вопрос-ответ




