В математике понятие предела играет ключевую роль и широко применяется в различных областях. Особенно важно понимание того, как предел функции стремится к нулю при приближении аргумента к определенной точке. Существует несколько способов доказательства этого факта, которые базируются на определениях предела и свойствах функций.
Одно из наиболее простых доказательств стремления предела к нулю основано на определении понятия предела. Согласно данному определению, предел \( \lim_{x \to a} f(x) = L \) означает, что для любого \(\varepsilon > 0\) существует \(\delta > 0\), такое что для всех \(x\) из проколотой окрестности \((a - \delta, a + \delta)\) выполняется условие \(|f(x) - L|
Применяя данное определение к пределу функции, стремящейся к нулю при приближении аргумента к некоторой точке, можно показать, что значение функции действительно приближается к нулю, когда аргумент стремится к этой точке. Это доказательство основывается на свойствах арифметики пределов и определении модуля разности.
Актуальность исследования стремления предела

Понимание процесса стремления предела к нулю играет важную роль в математике, физике и других науках. Стремление предела позволяет определить поведение функций и последовательностей в пределе, что имеет огромное практическое значение. Это понятие используется для анализа сложных систем, описания траекторий движения материальных объектов и других задач.
С помощью исследования стремления предела можно предсказать различные явления в природе, определить точные значения физических величин и провести анализ экономических и социальных процессов. Поэтому данная тема актуальна не только для ученых и математиков, но и для всех, кто стремится понять и объяснить законы природы и общества.
Теорема о стремлении предела функции

Теорема утверждает, что если функция f(x) стремится к пределу L при x стремящемся к a, то существует такое число δ > 0, что для любого числа ε > 0 существует число х=a+δ такое, что для всех х, удовлетворяющих условиям |x-a|
Это означает, что значения функции f(x) могут быть сколь угодно близкими к L, если только значения x достаточно близки к a.
Эта теорема является основой многих математических доказательств и помогает установить стремление функций к определенным значениям в пределе.
Определение предела функции

Предельное значение может быть бесконечным, конечным или не существовать вовсе. Для того чтобы убедиться в существовании предела, необходимо анализировать поведение функции при стремлении аргумента к определенной точке.
Предел функции может быть определен как односторонний (слева или справа) или двусторонний (с обеих сторон) в зависимости от направления приближения аргумента к точке.
Анализ стремления предела к максимуму
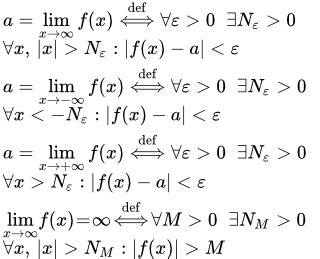
При изучении пределов функций важно не только понимать их стремление к нулю, но также обращать внимание на случаи, когда предел стремится к максимуму.
Когда функция приближается к конкретному числу при стремлении независимой переменной к определенному значению, говорят, что предел функции стремится к максимуму.
Для анализа стремления предела к максимуму необходимо учитывать характер функции и ее поведение в окрестности заданной точки. Использование графиков и алгебраических методов позволяет точно определить, к какому значению стремится предел при заданных условиях.
Таким образом, понимание стремления предела к максимуму играет важную роль в анализе функций и их поведения в точках с особым значением.
Влияние предела на асимптоты
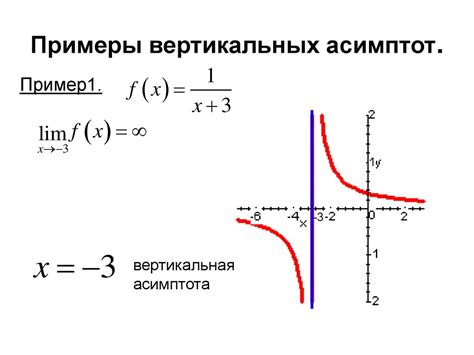
Если предел функции приближается к нулю, то функция может иметь асимптоту, параллельную оси абсцисс. Если предел функции стремится к бесконечности или минус бесконечности, то асимптоты могут быть горизонтальными или наклонными в зависимости от знака предела.
Изучение пределов функций помогает понять, как функция ведет себя при стремлении аргумента к определенным значениям или бесконечности, что важно для анализа ее асимптотического поведения и свойств.
Практическое применение стремления предела

Кроме того, стремление предела к нулю используется при изучении пределов последовательностей и рядов. На практике это позволяет анализировать поведение функций и выявлять их свойства, такие как непрерывность, дифференцируемость и корректную аппроксимацию значений функции.
В физике стремление предела играет важную роль при анализе предельных условий и приближенных моделей. Например, при изучении движения тела при малых скоростях или приближениях тела к нулевым массам.
Исследование сходимости к нулю

| Пример | Предел |
|---|---|
| f(x) = x^2 | lim(x->0) x^2 = 0 |
| f(x) = 1/x | lim(x->0) 1/x = ∞ |
| Последовательность a_n = 1/n | lim(n->∞) 1/n = 0 |
Таким образом, исследование сходимости позволяет определить характер стремления функции или последовательности к нулю и доказать утверждения о пределе.
Вопрос-ответ

Почему стремление предела к нулю важно в математике?
Доказательство стремления предела к нулю играет важную роль в математике, так как позволяет определить, насколько близко значение функции подходит к конкретному числу. Это понятие широко используется при изучении пределов, непрерывности функций и различных математических моделей.
Как можно начать доказательство стремления предела к нулю?
Доказательство стремления предела к нулю обычно начинается с определения предела функции. Затем следует использовать эпсилон-дельта определение, где для любого эпсилон больше нуля можно найти такое число дельта больше нуля, что каждое x находится в интервале (a-delta, a+delta) приводит значение функции к интервалу (L-epsilon, L+epsilon).
Какие примеры можно привести для иллюстрации стремления предела к нулю?
Примерами стремления предела к нулю могут служить функции вида f(x) = x/n при n стремящемся к бесконечности. В этом случае значение функции приближается к нулю по мере увеличения аргумента x. Также можно рассмотреть функцию 1/n, которая стремится к нулю при n стремящемся к бесконечности.



