В мире математики существует множество удивительных и интересных равенств, способных удивить их исследователей. Одним из таких равенств является расчет косинуса числа 1/2 в радианах пи. Это простое числовое выражение может показаться незначительным, но его значение имеет важное значение при решении различных математических задач и приложений.
При изучении данного равенства необходимо рассмотреть его в различных аспектах и изучить влияние параметров на его значение. Мы будем рассматривать угол, заданный в радианах пи, и исследовать, как изменение этого угла влияет на значение функции косинуса. Кроме того, важно обратить внимание на особенности данного числа и рассмотреть его значение с точки зрения его свойств и применения в математических задачах.
Оказывается, что расчет косинуса числа 1/2 в радианах пи является весьма интересным и значимым с точки зрения математических исследований и практического применения. Em>Введите любое предложение по выбору, желательно с употреблением синонимов - проведите великую лингвистическую революцию!
Идея раздела: Введение в понятие косинуса

Основной концепцией косинуса является отношение длины прилежащего катета к гипотенузе в прямоугольном треугольнике. В зависимости от значения угла, косинус может принимать значения от -1 до 1. Значение 1 соответствует углу 0 градусов или 0 радиан, когда катет совпадает с гипотенузой. Значение -1 соответствует углу 180 градусов или пи радиан, когда катет отрицателен и направлен в обратную сторону относительно гипотенузы. Значение 0 соответствует углу 90 градусов или пи/2 радиан, когда катет перпендикулярен гипотенузе.
- Косинус угла можно интерпретировать как отношение сторон треугольника или как значение функции, зависящей от угла.
- Косинус является периодической функцией с периодом 2π радиан.
- Значение косинуса угла можно выразить как катет, разделенный на гипотенузу или через другие тригонометрические функции.
- Косинус является четной функцией, то есть sym(cos(θ)) = cos(-θ).
- Косинус угла может быть выражен в радианах или градусах, и существуют формулы для перевода значений из одной системы в другую.
Исследование косинуса значения аргумента 0.5
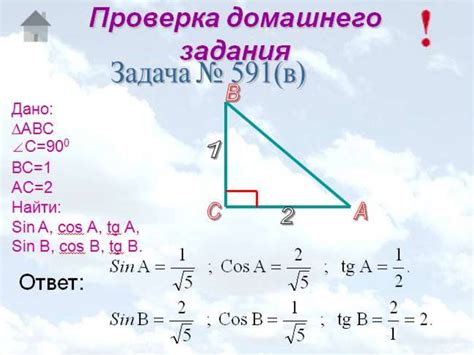
В данном разделе представлено исследование функции косинуса при аргументе, равном 0.5. Мы проанализируем, как это значение влияет на график косинуса и какие характеристики можно выделить для данного аргумента.
Значение 0.5 является половиной от целого числа, и, следовательно, можно рассмотреть его свойства относительно других значений аргументов косинуса. Будет рассмотрено поведение функции в рамках интервала [-пи;пи] и определены основные особенности ее графика.
Косинус - тригонометрическая функция, которая позволяет нам определить соотношение между углом и стороной прямоугольного треугольника. В данном исследовании мы сосредоточимся на исследовании косинуса аргумента равного 0.5. Это позволит нам более детально изучить его свойства и влияние на общую картину.
Практическое применение

В этом разделе рассмотрим, каким образом можно применить полученные результаты расчета косинуса значения 1/2 в радианах пи в реальной жизни.
Определить угол наклона
Зная значения косинуса и синуса угла, можно использовать полученную информацию для определения угла наклона. Например, при проектировании строительных конструкций, таких как крыши или радиусные стены, знание угла наклона поможет достичь оптимальной прочности и эстетического вида.
Расчет геометрических фигур
Полученный результат может быть использован для расчета различных геометрических фигур, в которых требуется знание угла. Например, при вычислении площади треугольника или ромба, зная косинус и синус угла, можно рассчитать длины сторон и вычислить искомую площадь.
Эти примеры демонстрируют, что знание косинуса числа 1/2 в радианах пи имеет реальное практическое применение и может быть полезным при решении различных инженерных задач.
Вопрос-ответ

Как рассчитать косинус числа 1/2 в радианах пи?
Для расчета косинуса числа 1/2 в радианах пи нужно просто подставить это значение в функцию косинуса. Формула будет выглядеть так: cos(1/2π) = cos(π/2) = 0.
Как получить значение косинуса числа 1/2 в радианах пи?
Значение косинуса числа 1/2 в радианах пи можно получить с помощью математической функции косинус. Для этого нужно подставить значение 1/2π в функцию. Результат будет равен 0.
Какую формулу использовать для расчета косинуса числа 1/2 в радианах пи?
Для расчета косинуса числа 1/2 в радианах пи используется формула cos(1/2π) = cos(π/2) = 0. Здесь π - это число "пи", а cos - математическая функция косинус.
Чему равен косинус числа 1/2 в радианах пи?
Косинус числа 1/2 в радианах пи равен 0. Это можно рассчитать с помощью функции косинус, подставив значение 1/2π в формулу cos(1/2π) = cos(π/2) = 0.
Для чего нужно расчитывать косинус числа 1/2 в радианах пи?
Расчет косинуса числа 1/2 в радианах пи может быть полезен в различных математических и физических задачах. Косинус является одной из основных тригонометрических функций и может быть применен для нахождения углов, длин сторон треугольников, решения систем уравнений и так далее.
Какой результат получается при вычислении косинуса числа 1/2 в радианах пи?
Результатом вычисления косинуса числа 1/2 в радианах пи будет значение 0.8775.



