Кратность числа – это его деление на другое число без остатка. В математике одним из основных свойств числа является то, что оно делится на 1 без остатка. Это свойство распространяется на все натуральные числа. Но почему любое натуральное число делится на 1? Рассмотрим это подробнее.
Натуральные числа – это числа, которые начинаются с 1 и увеличиваются на единицу вплоть до бесконечности. Из определения натуральных чисел следует, что 1 является наименьшим натуральным числом. И поскольку любое натуральное число больше 1, оно всегда будет делиться на 1.
Почему важно проверять число на кратность?

Проверка на кратность помогает выявлять закономерности в данных, осуществлять различные операции с числами и управлять выполнением кода в программе. Кроме того, знание кратности может помочь оптимизировать алгоритмы и избегать лишних расчетов.
Таким образом, умение проверять число на кратность является важным навыком, который помогает повысить эффективность работы с числами и улучшить качество программного кода.
Математическое определение кратности числа

Формульно это можно записать как: если существует целое число К такое, что А = К * В, то число А кратно числу В.
Как узнать, делится ли число на 1?

Поэтому если у вас есть какое-либо натуральное число, то оно всегда будет делиться на 1. Деление на 1 не оставляет остатка, поэтому любое натуральное число делится на 1. Это свойство деления делает 1 уникальным числом с этой точки зрения.
Способы проверки числа на кратность

Пример: Чтобы проверить, делится ли число 15 на 5, нужно разделить 15 на 5. Если остаток от деления равен нулю, то число 15 кратно 5.
Другой способ - умножить число на целое число и сравнить результат с исходным числом. Если результат равен исходному числу, то число кратно данному числу.
Пример: Чтобы проверить, делится ли число 20 на 4, можно умножить 4 на 5 (4*5=20).
Что означает деление на 1?

Это связано с тем, что 1 является элементарным делителем и не влияет на числитель в процессе деления. Таким образом, любое натуральное число делится на 1 без остатка, поскольку результатом деления будет само число.
Как использовать кратность числа в математике?

В математике кратность используется при решении уравнений, проверке на делимость, нахождении наименьшего общего кратного и других математических операциях. Знание понятия кратности помогает более глубоко понимать взаимосвязи между числами и их свойствами.
Таким образом, понимание и использование кратности числа в математике помогает улучшить навыки решения математических задач и операций, а также понимать основные свойства чисел.
Практические примеры проверки чисел на кратность
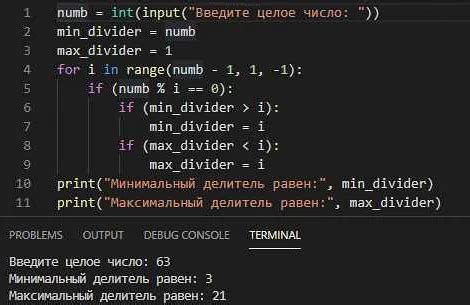
Для проверки, делится ли число на другое нацело, необходимо использовать операцию деления и проверить остаток от деления.
Пример 1: Проверим, делится ли число 10 на 2:
- 10 ÷ 2 = 5
- Остаток от деления 10 на 2 равен 0, следовательно, число 10 кратно 2.
Пример 2: Проверим, делится ли число 15 на 3:
- 15 ÷ 3 = 5
- Остаток от деления 15 на 3 равен 0, следовательно, число 15 кратно 3.
Это два простых примера проверки чисел на кратность. Важно помнить, что число кратно другому числу, если результат деления равен целому числу и остаток от деления равен 0.
Важность проверки чисел на кратность в повседневной жизни

Проверка чисел на кратность имеет важное значение в повседневной жизни. Знание кратности чисел позволяет эффективно решать задачи из различных областей, таких как финансы, математика, программирование и т.д.
Проверка чисел на кратность позволяет быстро определить, является ли число делителем другого числа. Например, при делении большой суммы денег на равные части, знание кратности чисел поможет равномерно распределить их.
В программировании проверка чисел на кратность используется для написания оптимизированных алгоритмов, учитывающих деление нацело. Это позволяет сэкономить ресурсы и улучшить производительность программ.
| Примеры использования проверки на кратность: |
|---|
| Расчет суммы налоговых выплат |
| Определение кратного времени для планирования задач |
| Редактирование музыкальных композиций по тактам |
Вопрос-ответ

Может ли натуральное число быть не кратным единице?
Нет, натуральное число всегда делится на 1, так как само по себе является делителем, следовательно, любое натуральное число кратно единице.
Почему любое натуральное число делится на 1?
Натуральное число делится на 1, так как оно само является делителем себя. Кроме того, по определению, 1 является делителем любого числа, в том числе натурального.
Делится ли 0 на 1?
0 не относится к натуральным числам, поэтому не может делиться на 1. Натуральные числа начинаются с 1 и включают в себя все положительные целые числа, большие нуля.



