Логарифм – это математическая функция, обратная к экспоненциальной функции. Однако, вопрос о взятии логарифма от отрицательного числа возникает довольно часто и вызывает некоторые трудности.
По определению, логарифм от числа равен степени, в которую нужно возвести число e (основание натурального логарифма) для получения этого числа. Но что делать, если мы пытаемся взять логарифм от отрицательного числа?
Давайте разберемся в этом вопросе подробнее и выясним, возможно ли взятие логарифма от отрицательного числа и какие особенности это может иметь.
Мифы и реальность

Существует миф о том, что нельзя взять логарифм от отрицательного числа. Однако на самом деле это не так. Логарифм отрицательного числа существует и определен математически.
Для комплексных чисел действуют другие правила, и логарифм отрицательного числа представляется в виде комплексных чисел. Таким образом, ограничения, касающиеся взятия логарифма от отрицательного числа, относятся в основном к вещественным числам.
- Миф: Нельзя взять логарифм от отрицательного числа.
- Реальность: Для комплексных чисел логарифм отрицательного числа определен и существует.
Определение логарифма

Логарифм определен для положительных чисел, ноль и дробных чисел. Для отрицательных чисел логарифм не определен в вещественных числах, так как нельзя возвести положительное число в степень и получить отрицательное число.
| Основание \(a\) | Положительное число \(x\) | Логарифм \(y = \log_a(x)\) |
|---|---|---|
| 2 | 8 | 3 |
| 10 | 1000 | 3 |
| 5 | 25 | 2 |
Существование комплексных логарифмов
Логарифмы комплексных чисел могут быть определены для всех ненулевых комплексных чисел.
Комплексный логарифм z есть функция ln(z) + i*arg(z), где ln(z) – натуральный логарифм модуля числа z, а arg(z) – аргумент числа z.
Таким образом, для отрицательных комплексных чисел также можно определить комплексный логарифм.
Это показывает, что комплексный логарифм является более общим понятием, чем действительный логарифм, и существует даже для отрицательных чисел.
Алгоритм вычисления логарифма от отрицательного числа
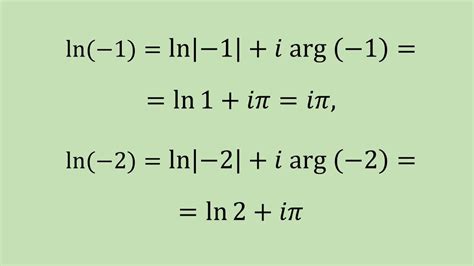
Для вычисления логарифма от отрицательного числа сначала необходимо понять, что логарифм отрицательного числа не существует в обычном смысле. Логарифмом числа x по основанию a называется степень, в которую нужно возвести основание a, чтобы получить число x. Однако логарифм отрицательного числа не имеет смысла в области вещественных чисел.
В математике также существует комплексный логарифм, который определен для всех комплексных чисел, включая положительные, отрицательные и нулевые. Для вычисления логарифма отрицательного числа в комплексной области используется формула:
ln(-x) = ln|x| + iπ
Где ln|x| - натуральный логарифм модуля отрицательного числа, а iπ - мнимая часть комплексного логарифма.
Таким образом, для вычисления логарифма отрицательного числа необходимо использовать комплексный логарифм и учитывать его мнимую часть.
Примеры вычислений

- Логарифм от -2: log(-2) не существует, так как логарифм определен только для положительных чисел.
- Логарифм от -5: log(-5) также не определен, поскольку логарифм отрицательного числа не имеет смысла в вещественных числах.
- Логарифм от -1: log(-1) также не является реальным числом, поскольку результатом будет мнимое число i*pi, где i - мнимая единица, а pi - число пи.
Применение в математике

Когда мы рассматриваем логарифм отрицательного числа, мы можем представить его в виде комплексного числа с модулем (абсолютной величиной) равным логарифму от модуля и аргументом равным аргументу от исходного числа. Это позволяет использовать логарифмы отрицательных чисел в решении различных задач, например, при работе с уравнениями, интегралами и прочими математическими операциями, где могут возникать комплексные числа.
Свойства логарифмов

Свойства логарифмов:
- Логарифм от произведения равен сумме логарифмов: \( \log_b(ab) = \log_b(a) + \log_b(b) \)
- Логарифм от частного равен разности логарифмов: \( \log_b\left(\frac{a}{b} ight) = \log_b(a) - \log_b(b) \)
- Логарифм от степени равен умножению логарифма на показатель степени: \( \log_b(a^n) = n \cdot \log_b(a) \)
- Смена основания логарифма происходит по формуле: \( \log_b(a) = \frac{\log_c(a)}{\log_c(b)} \)
Вопрос-ответ

Можно ли взять логарифм от отрицательного числа?
Нет, нельзя взять логарифм от отрицательного числа в действительных числах. Логарифм от отрицательного числа не определен в вещественной математике. Логарифмы определены только для положительных вещественных чисел и нуля.
Почему не стоит пытаться взять логарифм отрицательного числа?
Попытка взять логарифм от отрицательного числа приводит к недопустимым операциям в действительных числах, так как логарифмы определены только для положительных вещественных чисел и нуля. Это противоречит математическому определению функции логарифма.



