Существует одна загадка, которая уже веками терзает исследователей геометрии. Это загадка о высоте треугольника, узкий проход в мире математических законов, где одно невероятное свойство за другим ломает все известные правила.
Многие из нас привыкли думать о треугольниках, они ассоциируются линиями, углами, сторонами. Но как насчет высоты? Говорят, что высота - это линия, проведенная от вершины треугольника к основанию, перпендикулярная плоскости, которой лежит треугольник. Все кажется простым и понятным, но на самом деле, это лишь вершина айсберга, который скрывает неисчерпаемый потенциал и волнующие загадки.
Представьте себе, что высота треугольника может быть не только кратчайшей, но и самой длинной стороной треугольника! Этот парадокс испытывает наше представление о треугольниках и заставляет нас переосмыслить все знания, которые мы считали безусловными и объективными.
Связь между высотой и сторонами треугольника

Этот раздел посвящен изучению взаимосвязи высоты и сторон треугольника. Мы рассмотрим, как величина высоты треугольника может быть зависима от длин его сторон и будем исследовать, какие закономерности можно обнаружить.
Высота треугольника - это перпендикуляр, опущенный из вершины треугольника к противоположной стороне. Она является важным аспектом геометрии треугольника и играет роль во многих математических расчетах.
Стороны треугольника - это отрезки, соединяющие вершины треугольника. Длины сторон могут быть разными, влияя на общую форму треугольника и его свойства.
В данном разделе будут рассмотрены различные способы вычисления высоты треугольника, используя его стороны. Будут представлены формулы и методы нахождения высоты треугольника, а также проведены соответствующие геометрические доказательства.
Для наглядности и понимания будут приведены примеры вычисления высоты и изменения ее значения при изменении длин сторон треугольника. Будет показано, как высота треугольника может быть как меньше, так и больше его сторон, в зависимости от геометрических условий.
Что такое вертикальная линия и как она помогает измерить перпендикулярность треугольника?

Для измерения высоты треугольника с помощью вертикальной линии необходимо провести линию, перпендикулярную одной из сторон треугольника и проходящую через противоположный угол. Это позволяет определить расстояние от данной стороны до противоположного угла и найти высоту треугольника.
- Шаг 1: Выберите одну из сторон треугольника, к которой вы хотите измерить высоту.
- Шаг 2: Проведите вертикальную линию, перпендикулярную выбранной стороне, так чтобы она проходила через противоположный угол.
- Шаг 3: Измерьте расстояние от выбранной стороны до точки пересечения с вертикальной линией.
Измеренное расстояние является высотой треугольника и может быть использовано для решения задач, требующих знания этого параметра. Изучение и практика измерения высоты треугольника позволяют лучше понять его геометрические свойства и применять их в практике.
Отношение высоты треугольника к его сторонам
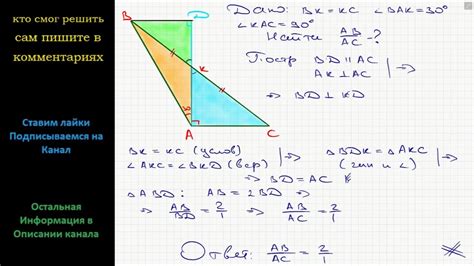
Важно подчеркнуть, что величина высоты может быть разная для различных треугольников и зависит от их формы и размеров. Но, несмотря на это, связь между высотой и сторонами треугольника всегда остается неизменной. Высота, соединяющая вершину треугольника с противоположной стороной, играет важную роль в определении его геометрических свойств.
Ученые занимаются исследованием различных соотношений между высотой треугольника и его сторонами. Они обращают внимание на влияние длины сторон на длину высоты и исследуют, как изменение этих параметров может влиять на свойства треугольника. В результате обширных исследований были выведены формулы и теоремы, которые позволяют более точно определить соотношения между высотой и сторонами треугольника.
Отношение высоты к сторонам является одним из важных индикаторов устойчивости треугольника. Малейшее изменение длин сторон может существенно повлиять на длину и положение высоты. Кроме того, высота треугольника имеет важное значение при вычислении его площади и нахождении других его геометрических характеристик.
Изучение отношения высоты треугольника к его сторонам предоставляет нам более глубокое понимание геометрических свойств этой фигуры. Наше исследование позволит более точно определить, какие параметры оказывают влияние на устойчивость треугольника и как эти свойства можно применить в различных практических задачах.
Случаи, когда высота треугольника не превышает его стороны
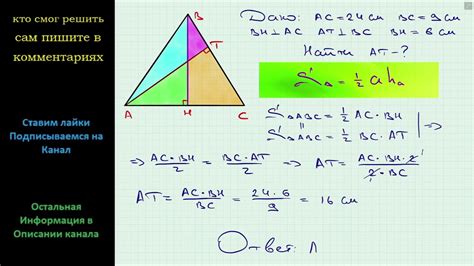
Рассмотрим особые ситуации, когда высота треугольника оказывается меньше длины его сторон. В этих случаях, геометрические свойства треугольника приводят к необычным результатам, которые стоит исследовать и понять.
Один из таких случаев - когда треугольник является остроугольным. В остроугольном треугольнике, углы при каждой из вершин оказываются меньше 90 градусов. В результате, высота, проведенная из острого угла к основанию, лежит внутри треугольника и сравнительно меньше его стороны. Это геометрическое свойство делает остроугольные треугольники уникальными и привлекательными для изучения.
Еще один интересный случай возникает, когда треугольник оказывается равнобедренным. В равнобедренном треугольнике две стороны, возле которых стоят равные углы, оказываются равными по длине. В результате, высота, проведенная из вершины равнобедренного треугольника к основанию, делит его на два равных отрезка, при этом сама высота является меньшей стороной треугольника. Это геометрическое свойство отличает равнобедренные треугольники от остальных и позволяет решать различные задачи, связанные с этим специальным типом треугольников.
Также можно обратить внимание на случай, когда треугольник является прямоугольным. В прямоугольном треугольнике, один из углов оказывается равным 90 градусов, а стороны, прилегающие к этому углу, называются катетами. Высота, проведенная из прямого угла к гипотенузе, будет меньше катетов и играет важную роль в решении задач на нахождение площади треугольника и его геометрические параметры.
| Тип треугольника | Условия | Геометрические свойства |
|---|---|---|
| Остроугольный треугольник | Все углы треугольника меньше 90 градусов | Высота лежит внутри треугольника и меньше его сторон |
| Равнобедренный треугольник | Две стороны, прилегающие к равным углам, равны по длине | Высота делит треугольник на две равные части и является меньшей длиной стороны |
| Прямоугольный треугольник | Один из углов треугольника равен 90 градусов | Высота, проведенная к основанию, является меньшей длиной катетов |
Вопрос-ответ

Вопрос
Ответ
Можно ли треугольник с равными сторонами иметь высоту, меньшую чем длина его стороны?
Нет, для треугольника с равными сторонами высота всегда равна половине длины одной из сторон. Такой треугольник называется равнобедренным.
Влияет ли острота углов треугольника на его высоту?
Да, острота углов треугольника может влиять на его высоту. В случае остроугольного треугольника, высота может быть представлена как отрезок, проходящий из вершины треугольника и перпендикулярный основанию.
Высота треугольника всегда меньше его стороны?
Нет, высота треугольника может быть как меньше, так и больше его стороны. В случае прямоугольного треугольника, одна из сторон является гипотенузой, и высота, проведенная к этой стороне, может быть больше, чем сама сторона.
Влияет ли длина сторон треугольника на его высоту?
Да, длина сторон треугольника может влиять на его высоту. Чем больше длина сторон, тем больше может быть высота треугольника. Однако, на самом деле, высота треугольника будет зависеть от самих сторон треугольника и его углов.



