В мире математики, где кажется, что каждое правило имеет свое исключение, некоторые связи между числами и геометрическими формами остаются по-настоящему загадочными и заинтриговывают умы исследователей. Одной из таких связей является запутанная и непостижимая связь между числом 76 и особым четырехугольником, известным как...
Особенность, лежащая в основе этой связи, легко ускользает от нашего восприятия на первый взгляд. Однако, при более близком рассмотрении и углубленном анализе, мы начинаем замечать странные соотношения и закономерности, которые открывают новые грани этой загадочной проблемы. Откуда берется число 76 и как оно связано с геометрическими формами?
Четырехугольник, с точностью до научного определения, является фигурой, состоящей из четырех сторон и четырех углов. Однако данный четырехугольник обладает свойством параллелограмма, что делает его особенным и интересным для анализа и исследования.
Определение параллелограмма и его основные свойства
Свойство №1: Параллельные стороны параллелограмма равны между собой. Это означает, что если взять любые две параллельные стороны этой фигуры и сравнить их длины, то они окажутся равными.
Свойство №2: Противоположные углы параллелограмма равны между собой. Если мы возьмем два противоположных угла этой фигуры и измерим их, то получим одинаковые значения.
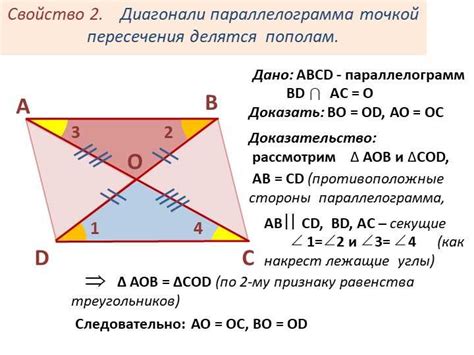
Свойство №3: Диагонали параллелограмма делятся пополам. Если соединить вершины параллелограмма диагоналями, то эти диагонали разделятся пополам, то есть их точка пересечения будет являться точкой деления каждой диагонали на две равные части.
Свойство №4: Параллелограмм имеет две пары параллельных сторон и две пары параллельных углов. Это позволяет нам использовать данные свойства для решения различных задач связанных с параллелограммами.
Вот основные свойства параллелограмма. Изучение этих свойств позволит понять его конструкцию и использовать их для решения задач геометрии и анализа пространственных фигур.
Определение четырехугольника-параллелограмма
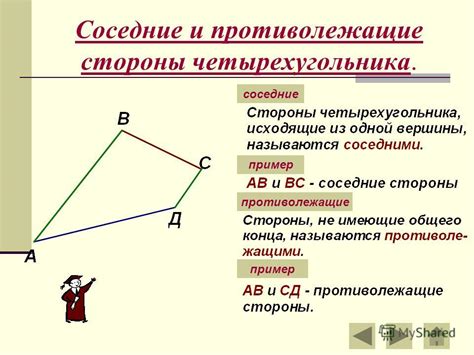
В геометрии существует определенный класс четырехугольников, который называется параллелограммами. Эти фигуры обладают некоторыми уникальными свойствами, которые позволяют их отличить от других четырехугольников.
Основная особенность параллелограмма заключается в том, что противоположные стороны этой фигуры параллельны друг другу. Это означает, что линии, проведенные через соответствующие концы этих сторон, никогда не пересекаются. Также параллелограмм имеет пары равных противоположных сторон и равные противоположные углы.
Четырехугольник-параллелограмм может быть как прямоугольным, так и непрямоугольным. В случае прямоугольного параллелограмма, все его углы равны 90 градусам, что делает его также прямоугольником. Непрямоугольный же параллелограмм имеет два пары углов, сумма которых равна 180 градусам.
По определению, параллелограмм - это четырехугольник с противоположными сторонами, которые параллельны друг другу, и равными противоположными углами. Такая фигура часто встречается в различных областях, включая геометрию, архитектуру, инженерное дело и другие.
- Противоположные стороны параллельны друг другу
- Противоположные стороны равны
- Противоположные углы равны
- Может быть прямоугольным или непрямоугольным
Изучение особенностей четырехугольника-параллелограмма помогает не только понять его геометрические свойства, но и применять его в различных задачах и конструкциях.
Основные свойства параллелограмма
1. Противоположные стороны параллельны.
Параллелограмм содержит две пары противоположных сторон, которые всегда параллельны друг другу. Это означает, что при продолжении этих сторон они никогда не пересекутся.
2. Противоположные стороны равны по длине.
Другим важным свойством параллелограмма является то, что его противоположные стороны равны по длине. Это означает, что если измерить длину одной пары противоположных сторон, то они окажутся одинаковыми.
3. Противоположные углы равны.
В параллелограмме также имеются противоположные углы, которые равны друг другу. Это означает, что если измерить угол между двумя противоположными сторонами, он окажется равным углу, образованному другой парой противоположных сторон.
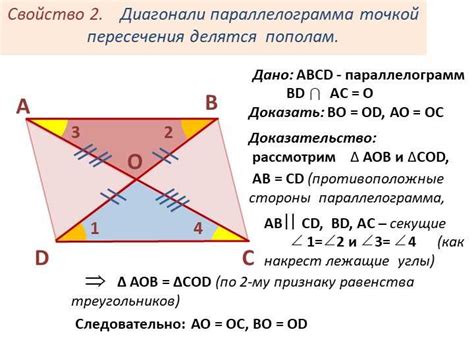
4. Диагонали параллелограмма делятся пополам.
В параллелограмме диагонали – это отрезки, соединяющие вершины, не лежащие на одной стороне. Интересно, что диагонали всегда делятся пополам, то есть точка пересечения диагоналей является их точкой деления в отношении 1:1.
Формула для вычисления периметра параллелограмма
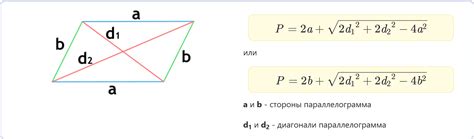
Периметр параллелограмма определяется как сумма длин всех его сторон. Для вычисления периметра необходимо знать длины сторон параллелограмма или иметь достаточно информации для их определения.
Чтобы найти периметр параллелограмма, мы можем использовать следующую формулу:
- Суммируем длины всех четырех сторон параллелограмма.
- Обозначим длины сторон как a, b, c и d.
- Тогда формула для вычисления периметра будет иметь вид: Периметр = a + b + c + d.
Например, если известны длины сторон a = 10, b = 15, c = 12 и d = 17, то периметр параллелограмма будет равен:
- Периметр = 10 + 15 + 12 + 17 = 54.
Таким образом, зная длины сторон параллелограмма или имея достаточную информацию для их определения, можно легко вычислить его периметр с помощью данной формулы.
Расчет периметра параллелограмма при известных сторонах и углах
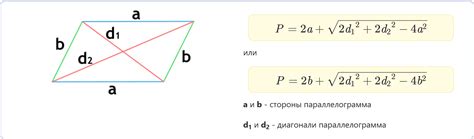
В данном разделе мы рассмотрим способы вычисления периметра параллелограмма, когда нам известны его стороны и углы.
Периметр параллелограмма - это сумма длин всех его сторон. Зная значения сторон и углов, мы можем применить соответствующие формулы, чтобы найти итоговый результат.
Одним из способов расчета периметра является сложение всех сторон параллелограмма. Если стороны параллелограмма обозначены соответственно как a, b, c и d, то периметр можно найти по формуле:
Периметр = a + b + c + d
В другом случае, когда нам известны стороны a и c параллелограмма, а также угол между ними, мы можем использовать теорему косинусов для нахождения длины боковой стороны. После этого, периметр можно вычислить, сложив все стороны параллелограмма.
Периметр = a + b + c + d
Однако, необходимо помнить, что в параллелограмме противоположные стороны равны между собой, что позволяет сократить вычисления.
Для удобства расчетов, можно использовать специализированные программы или онлайн калькуляторы, которые автоматически выполняют все необходимые вычисления.
В итоге, зная значения сторон и углов параллелограмма, мы можем точно рассчитать его периметр и использовать эту информацию в различных практических задачах.
Пример вычисления периметра параллелограмма при заданных значениях сторон и угла
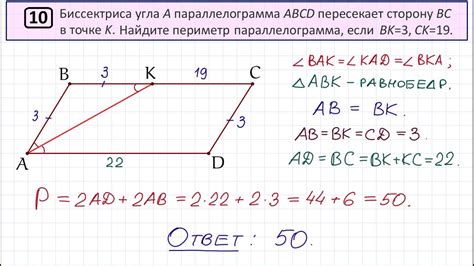
Для начала определим, какие значения у нас имеются. Пусть стороны параллелограмма обозначаются как a и b, а величина угла между этими сторонами обозначается как α. Давайте назовем периметр параллелограмма как Р.
| Параметр | Обозначение | Значение |
|---|---|---|
| Длина стороны a | a | здесь введите значение |
| Длина стороны b | b | здесь введите значение |
| Угол α | α | здесь введите значение |
Периметр параллелограмма определяется как сумма всех его сторон. В нашем случае, мы имеем две стороны параллелограмма - a и b - которые равны по величине, и еще две стороны с такой же длиной в силу параллельности. Таким образом, можно записать:
Р = 2a + 2b
Однако, у нас также есть информация о величине угла α. Это означает, что мы должны учесть данный угол при вычислении периметра. Для этого стоит использовать тригонометрические функции, такие как синус и косинус.
Итак, чтобы учесть угол α при вычислении периметра, мы можем записать:
Р = 2(a + b) + 2(a * cos(α))
В данном выражении мы учитываем две стороны с длиной a и две стороны с длиной b, а также добавляем произведение одной из сторон на косинус угла α.
Используя данные значения сторон и угла, вы можете вычислить периметр параллелограмма по данной формуле.
Формула для вычисления площади параллелограмма
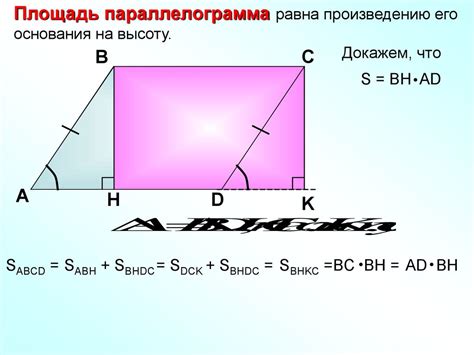
Для вычисления площади параллелограмма существует простая формула: "Площадь = сторона a * высота h".
В данной формуле сторона a представляет собой длину одной из сторон параллелограмма, а высота h - перпендикулярную расстояние от этой стороны до противоположной стороны.
Полученное значение площади параллелограмма, выраженное в квадратных единицах, позволяет оценить его размер и величину, а также использовать при решении различных геометрических задач.
Расчет площади параллелограмма при известных сторонах и углах
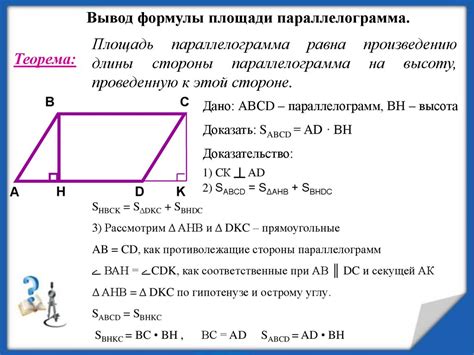
Для расчета площади параллелограмма при известных сторонах и углах мы можем использовать различные формулы и методы. Одним из наиболее простых способов является расчет площади по формуле: площадь равна произведению длин двух сторон на синус угла между ними.
Для более сложных случаев, когда известны не только стороны, но и углы параллелограмма, мы можем воспользоваться формулой Герона. Она позволяет найти площадь фигуры, зная длины всех ее сторон и диагоналей. Этот метод применяется, когда есть информация обо всех величинах, необходимых для расчета.
Важно помнить, что при расчете площади параллелограмма необходимо учитывать единицы измерения и преобразовывать их, если они отличаются. Также стоит отметить, что полученное значение площади будет иметь ту же размерность, что и исходные стороны и углы.
Зная различные методы и формулы для расчета площади параллелограмма при известных сторонах и углах, мы можем более точно определить его площадь и использовать эту информацию в различных практических задачах.
Вопрос-ответ

Что такое параллелограмм?
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине.
Как определить, является ли данный четырехугольник параллелограммом?
Чтобы определить, является ли четырехугольник параллелограммом, необходимо проверить, являются ли противоположные стороны параллельными и равными по длине. Также можно проверить, являются ли противоположные углы равными. Если все эти условия выполняются, то четырехугольник является параллелограммом.
Как найти длину диагонали параллелограмма, если известна длина стороны и длина высоты?
Если известна длина стороны параллелограмма и длина высоты, то можно найти длину диагонали, используя теорему Пифагора. Длина диагонали равна корню квадратному из суммы квадратов длины стороны и высоты, умноженных на 2.
Можно ли найти длину диагонали параллелограмма, зная только одну из диагоналей?
Да, можно. Если известна длина одной из диагоналей параллелограмма, то длина другой диагонали можно найти, используя теорему Пифагора. Длина диагонали равна корню квадратному из разности квадратов длины стороны и длины известной диагонали.
Как найти периметр параллелограмма, зная длины его сторон?
Периметр параллелограмма можно найти, сложив длины всех его сторон. Если даны длины всех сторон, то периметр равен сумме этих длин.



