Функция y=x^2 - одна из наиболее известных и простых функций в математике. Степенная функция второй степени вызывает множество вопросов у студентов математики: является ли она монотонной или нет?
Для понимания, является ли функция y=x^2 монотонной, необходимо разобраться в ее поведении на промежутке действительных чисел. Рассмотрим изменение функции в зависимости от значения x.
Исследование монотонности функции y=x^2 позволит понять, какой характер изменения принимает график этой функции. Давайте разберемся в деталях и выясним, является ли функция y=x^2 монотонной или нет!
Монотонность функции
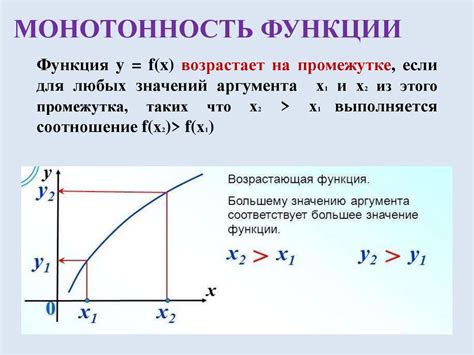
Монотонность функции означает изменение ее значений по мере изменения аргумента. Если функция всегда убывает или возрастает при всех значениях аргумента, то она называется строго монотонной.
Для функции y=x^2 можно определить монотонность, анализируя производную. Заметим, что производная функции y=x^2 равна 2x. Если производная положительна при всех значениях x, то функция возрастает (строго возрастает). Если производная отрицательна при всех значениях x, то функция убывает (строго убывает). Таким образом, функция y=x^2 является строго возрастающей при x>0 и строго убывающей при x
Понятие монотонности функции
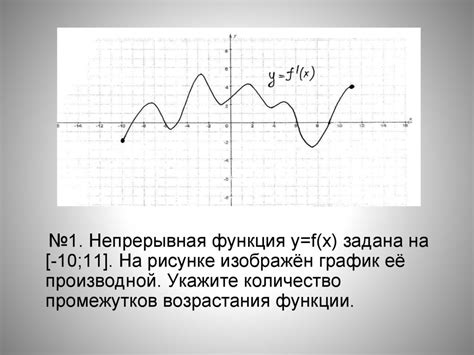
График функции y=x^2 не является монотонным, так как он одновременно увеличивается на промежутках x>0 и уменьшается на промежутках x
Функция y=x^2
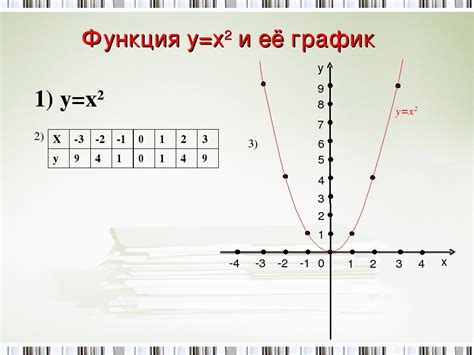
Эта функция не является монотонной, так как при увеличении x значения y увеличиваются при x>0 и уменьшаются при x
Исследование монотонности

Для исследования монотонности функции y=x^2 проведем анализ производной.
1. Найдем производную функции: y' = 2x.
2. Теперь определим знак производной в различных интервалах:
- Если x
- Если x = 0, то y' = 0, что указывает на точку экстремума.
- Если x > 0, то y' > 0, что говорит о возрастании функции.
Таким образом, функция y=x^2 возрастает при x > 0 и убывает при x
График функции y=x^2
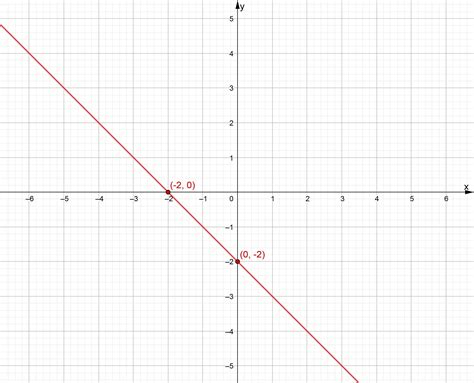
График функции \(y=x^2\) представляет собой параболу, которая открывается вверх, если коэффициент при квадратичном члене положителен.
Вершина параболы находится в точке (0,0). Парабола симметрична относительно оси y, то есть при отражении относительно этой оси получится та же парабола.
Поведение графика зависит от знака коэффициента при квадратичном члене. В случае \(y=x^2\), график возрастает на всей области определения (для всех x), поэтому функция \(y=x^2\) неубывающая.
Доказательство монотонности
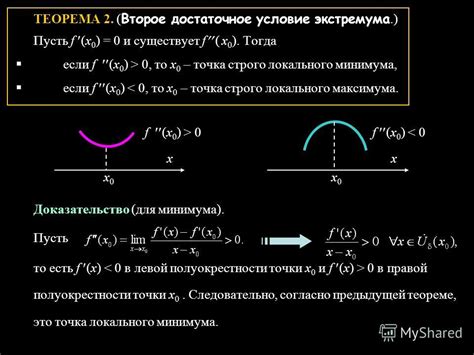
Для доказательства монотонности функции y=x^2 необходимо проанализировать производную данной функции. Вычислим производную функции y=x^2:
y' = d/dx (x^2) = 2x
Производная функции равна 2x. Рассмотрим знак производной в различных интервалах значений x:
1. Если x>0, то производная y' положительна (2x>0), что указывает на монотонное возрастание функции в этом интервале.
2. Если x
Таким образом, функция y=x^2 монотонно возрастает при x>0, монотонно убывает при x
Таким образом, можно заключить, что функция y = x^2 не обладает однозначно определенной монотонностью на всей области определения.
Вопрос-ответ

Почему функция y=x^2 монотонная или нет?
Функция y=x^2 не является монотонной, потому что она возрастает на интервалах [0; +∞) и убывает на интервалах (-∞; 0].
Какие интервалы функции y=x^2 являются монотонными?
Функция y=x^2 монотонна на интервалах [0; +∞) и (-∞; 0], так как возрастает на первом и убывает на втором.
Почему производная функции y=x^2 равна нулю в точке x=0?
Производная функции y=x^2 равна 2x. В точке x=0 производная равна нулю, так как это точка экстремума (минимума) - парабола имеет минимум в этой точке именно потому, что производная в ней равна нулю.
Чему равны приращения функции y=x^2 при увеличении х на единицу?
Приращение функции y=x^2 при увеличении х на единицу равно разности значений функции в точках x+1 и x: (x+1)^2 - x^2 = 2x + 1.
В какой точке функции y=x^2 происходит разворот графика?
Разворот графика функции y=x^2 происходит в точке x=0, так как в этой точке меняется направление монотонности функции с возрастания на убывание, и наоборот.



