Синус – одна из основных тригонометрических функций, которая играет важную роль в математике и физике. Возникает вопрос: является ли синус четной или нечетной функцией?
Чтобы ответить на этот вопрос, вспомним определение четной и нечетной функции. Четная функция обладает свойством f(-x) = f(x) для всех x из области определения, а нечетная функция – f(-x) = -f(x). Подставляя значения в синус, мы можем определить его тип.
Существование синуса как функции
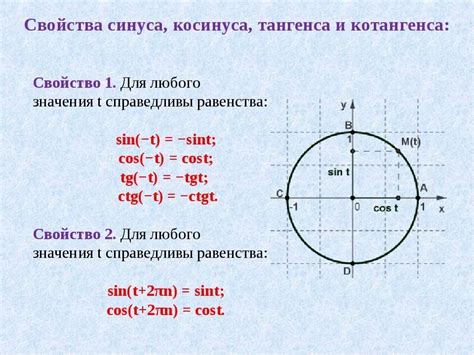
Важно отметить, что синус является четной функцией, что означает, что синус отрицательного угла равен синусу соответствующего положительного угла. Это свойство делает синус удобным инструментом для анализа периодических явлений в физике, математике и других науках.
Синус имеет множество приложений в различных областях, таких как оптика, акустика, электроника и другие. Понимание свойств и характеристик синуса помогает в решении различных задач и уравнений.
Определение понятия "синус"
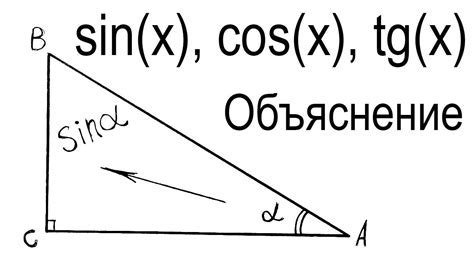
Математически обозначается символом sin(x), где x – угол, по отношению к синусу которого производится вычисление.
Синус является периодической функцией с периодом 2π и принимает значения в диапазоне от -1 до 1.
Математическое представление синуса
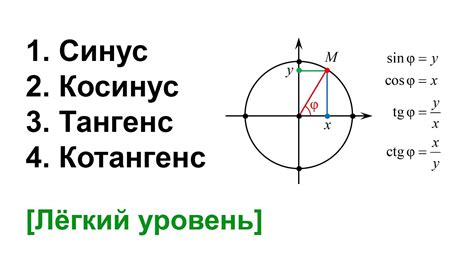
Математическое представление синуса:
Для любого угла α (в радианах) справедливо:
sin(α) = y/r, где y - противолежащий катет, r - радиус окружности с центром O(0,0) и точкой касания на границе окружности на единичном угле.
Четность функции синуса

Таблица признаков четности и нечетности для различных функций поможет лучше понять свойства функции синуса:
| Функция | Четность | Нечетность |
|---|---|---|
| Синус (sin(x)) | Нечетная | Да |
Симметрия графика синуса
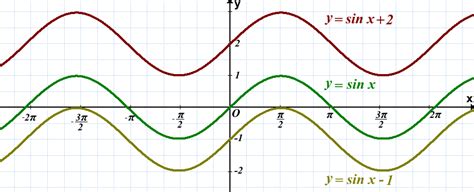
Благодаря этому свойству график синуса симметричен относительно начала координат. Точка (-x, -sin(x)) лежит на графике симметрично точке (x, sin(x)). Данная симметрия делает график синусоиды отражательно нечетным.
Таким образом, симметрия графика синуса является важным свойством, которое легко наблюдается на плоскости и помогает визуально представить характер функции.
Доказательство четности синуса
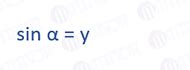
| Утверждение | Доказательство |
| Синус – нечетная функция | Рассмотрим синус угла $-\theta$: $\sin(-\theta) = -\sin(\theta)$ (по определению синуса) Таким образом, $\sin(-\theta) = -\sin(\theta)$, что означает, что синус – нечетная функция. |
Синус как периодическая функция
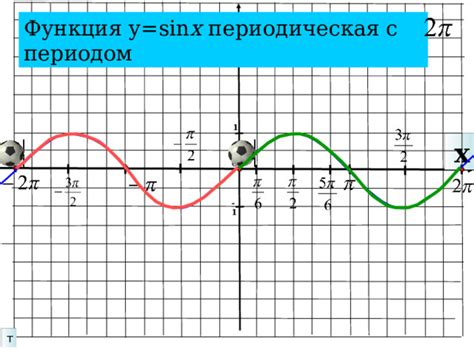
- Периодичность: Синус имеет период 2π, то есть его значение повторяется каждые 2π радиан или 360°.
- Четность: Синус не является четной функцией, так как sin(-x) ≠ -sin(x). Это означает, что график синуса не симметричен относительно оси ординат.
- Нули: Нулями синуса являются точки, в которых он равен нулю. Первый ноль синуса находится в точке x = 0, следующие нули повторяются через каждый период.
Изучение синуса как периодической функции имеет важное значение в математике, физике, астрономии и других науках, где применяются колебания и волны.
Периодичность графика синуса
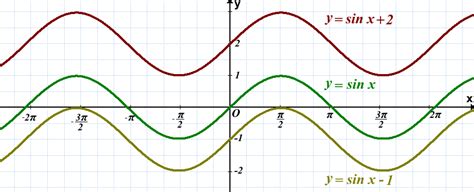
Синусоидальная функция синус имеет периодичность, то есть при изменении аргумента на $2\pi$ значение функции повторяется. График синуса повторяется каждые $2\pi$ радиан, что делает его периодической функцией.
Таким образом, график синуса будет повторяться снова и снова каждые $2\pi$ радиан, образуя характеристическую волну. Можно сказать, что синус - это периодическая функция с периодом $2\pi$ и она является четной функцией.
Повторяемость значений синуса
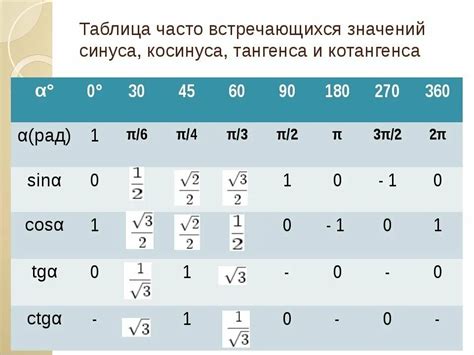
Таким образом, значения синуса повторяются каждые ${2\pi}$ радиан, что делает его повторяющимся и предсказуемым способом вычисления его значений в различных точках.
Применение синуса в математике
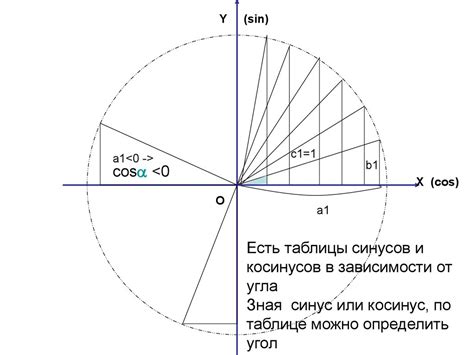
- Тригонометрия: Синус играет ключевую роль в тригонометрии, помогая связывать углы и стороны в треугольниках, а также в решении различных задач на плоскости.
- Математический анализ: Синус используется в дифференциальном и интегральном исчислении, например, при нахождении производных и интегралов от функций.
- Физика и инженерия: В различных физических и инженерных задачах синус используется для описания колебательных процессов, электрических и механических волн, а также при моделировании различных систем.
- Компьютерная графика: Синус применяется для создания различных визуальных эффектов, анимации и трансформаций объектов в компьютерной графике.
Угловая мера в тригонометрии
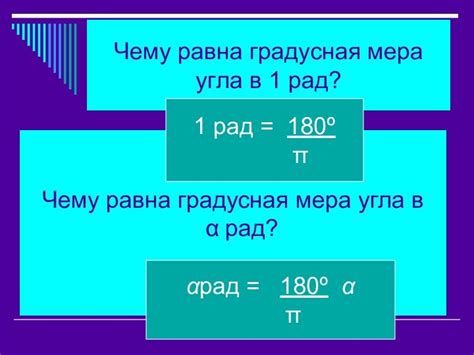
Один радиан соответствует углу, при вершине которого длина дуги окружности равна длине радиуса. Таким образом, угол в один радиан охватывает длину радиуса окружности.
При расчетах в тригонометрии обычно используют радианы, так как они позволяют связать углы с длиной дуги и с участием математических функций, таких как синус, косинус и тангенс.
Решение уравнений с использованием синуса

Вопрос-ответ

Синус — четная функция или нет?
Синусная функция не является четной функцией. Четная функция обладает свойством f(x) = f(-x) для любого x в области определения функции. Для синуса это свойство не выполняется: sin(-x) = -sin(x), поэтому синус — нечетная функция.
Как можно определить, является ли синус четной или нечетной функцией?
Для того чтобы определить, является ли функция четной или нечетной, необходимо проверить выполнение условия f(x) = f(-x) для четной функции и f(x) = -f(-x) для нечетной. В случае с синусом мы видим, что sin(-x) = -sin(x), что означает, что синус — нечетная функция.
Почему синусная функция является нечетной?
Синусная функция не является четной из-за свойства sin(-x) = -sin(x). Это означает, что для отрицательного значения угла синус будет равен минус синусу от положительного угла, что является характеристикой нечетной функции.
Если синусная функция нечетная, то какие другие тригонометрические функции четны?
Синус — это нечетная функция, а косинус — четная функция. Также тангенс и котангенс являются нечетными функциями, а секанс и косеканс — четными.



