В мире математики существует множество интересных и загадочных чисел. Одним из любопытных вопросов является связь между числами и их взаимной простотой. В этой статье мы разберемся, являются ли числа 104 и 121 взаимно простыми или нет.
Для того, чтобы узнать, являются ли два числа взаимно простыми, необходимо проверить их на наличие общих делителей, отличных от единицы. В данном случае, числа 104 и 121 представляют собой квадраты некоторых чисел - 10 и 11 соответственно.
Как это отразится на их взаимной простоте? Давайте вместе разберемся и узнаем, являются ли числа 104 и 121 взаимно простыми, или у них есть общие делители!
Анализ простых чисел 104 и 121
104 и 121: основные характеристики
Давайте рассмотрим основные характеристики чисел 104 и 121:
| Число | 104 | 121 |
| Простое или составное | Составное | Составное |
| Делители | 1, 2, 4, 8, 13, 26, 52, 104 | 1, 11, 121 |
| Сумма делителей | 206 | 133 |
| Квадратный корень | 10.198 | 11 |
Разложение числа 121 на множители
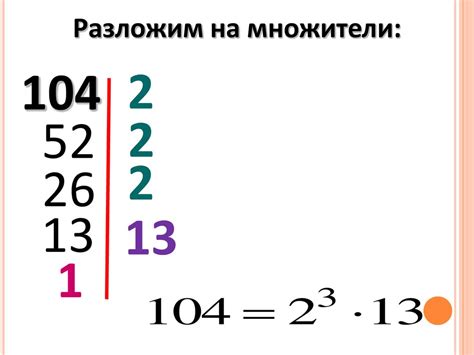
Таким образом, разложение числа 121 на множители будет следующим: 121 = 11 * 11. Это означает, что 11 - это единственный множитель числа 121.
И 121: связь с другими числами
Когда рассматриваем число 104, оно не является квадратом целого числа, но можно заметить, что 104 = 8 * 13. Оба числа 8 и 13 являются простыми числами, но 104 само по себе не является простым числом, так как имеет делители отличные от 1 и самого себя.
Таким образом, число 104 и число 121 не являются взаимно простыми. Они имеют общий делитель - число 8. Несмотря на это, каждое из них все же является простым, что делает их числа интересными в мире математики.
Математические операции с числами 104 и 121
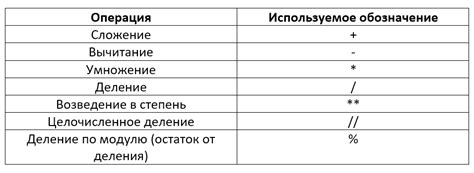
- Найти наибольший общий делитель (НОД). Для чисел 104 и 121 НОД равен 1, что свидетельствует о их взаимной простоте.
- Проверить их простоту. Число 104 не является простым, поскольку имеет делители (1, 2, 4, 8, 13, 26, 52). Число 121 также не является простым, его делители это (1, 11, 121).
- Посчитать количество общих делителей. С числами 104 и 121 у них есть общий делитель - единица. Поэтому они взаимно простые.
Таким образом, числа 104 и 121 действительно являются взаимно простыми числами.
Числа 104 и 121: простота или составные числа?

104 и 121: теорема Эйлера и числа Ферма

Теорема Эйлера утверждает, что если два числа являются взаимно простыми, то их произведение на одно меньше, чем число, даёт остаток 1 при делении на это число. Числа 104 и 121 имеют общий делитель, поэтому они не удовлетворяют условию теоремы Эйлера.
Числа Ферма являются особыми числами в теории чисел, которые обладают рядом интересных свойств. Одно из них утверждает, что для простого числа p и целого числа a, взаимно простого с p, выполняется сравнение a^(p-1) ≡ 1 (mod p). Для чисел 104 и 121 это утверждение также не выполняется.
И 121: применение в современной математике
Число 121, являющееся квадратом числа 11, также имеет интересные свойства в математике.
Одним из применений числа 121 является его использование в качестве простого числа для проверки алгоритмов и методов работы с простыми числами. Так как 121 – это квадрат простого числа 11, его простота позволяет применять его в математических вычислениях и исследованиях.
Помимо этого, число 121 также встречается в различных комбинаторных задачах, а также может использоваться в криптографии и теории чисел.
Таким образом, число 121, несмотря на свою простоту и относительно небольшое значение, имеет разнообразные применения в современной математике и является объектом интереса для исследований и анализа.
Для дальнейших исследований и математических расчетов рекомендуется учитывать это свойство чисел 104 и 121 при проведении анализа и вычислений, чтобы избежать ошибок и путаницы в результатах.
Вопрос-ответ

Чему равно произведение чисел 104 и 121?
Произведение чисел 104 и 121 равно 12584.
Являются ли числа 104 и 121 взаимно простыми?
Числа 104 и 121 не являются взаимно простыми, так как у них есть общий делитель - число 1 и само число 1, следовательно, они не взаимно простые.
Сколько существует натуральных чисел, взаимно простых с числом 104?
Чтобы найти количество натуральных чисел, взаимно простых с числом 104, используют функцию Эйлера. Эта функция обозначается как φ(104) и показывает количество чисел, менее чем 104, которые не имеют общих делителей с 104, кроме 1. Таким образом, φ(104) = 40. Получается, что с числом 104 взаимно простых 40 натуральных чисел.



